
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:高中数学 来源: 题型:选择题
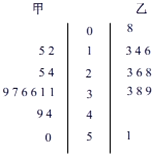 如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.则甲、乙两名运动员成绩比较( )
如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.则甲、乙两名运动员成绩比较( )| A. | 甲比乙稳定 | B. | 乙比甲稳定 | ||
| C. | 甲、乙稳定程度相同 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
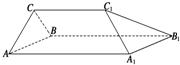 如图所示的几何体中,四边形AA1B1B是边长为3的正方形,CC1=2,CC1∥AA1,这个几何体是棱柱吗?若是,指出是几棱柱.若不是棱柱,请你试用一个平面截去一部分,使剩余部分是一个棱长为2的三棱柱,并指出截去的几何体的特征,在立体图中画出截面.
如图所示的几何体中,四边形AA1B1B是边长为3的正方形,CC1=2,CC1∥AA1,这个几何体是棱柱吗?若是,指出是几棱柱.若不是棱柱,请你试用一个平面截去一部分,使剩余部分是一个棱长为2的三棱柱,并指出截去的几何体的特征,在立体图中画出截面.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
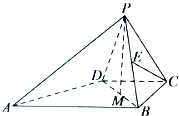 如图,四棱锥P-ABCD中,∠ABC=∠BCD=90°,AB=2,CD=CB=CP=1.点P在底面上的射影为线段BD的中点M.
如图,四棱锥P-ABCD中,∠ABC=∠BCD=90°,AB=2,CD=CB=CP=1.点P在底面上的射影为线段BD的中点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.6 | 3.0 | 3.3 | 4.1 | 4.5 | 4.9 | 5.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$+$\overrightarrow{BC}$ | B. | $\overrightarrow{AD}$+$\overrightarrow{EB}$+$\overrightarrow{BC}$+$\overrightarrow{CE}$ | C. | $\overrightarrow{MB}$-$\overrightarrow{MA}$+$\overrightarrow{BD}$ | D. | $\overrightarrow{CB}$+$\overrightarrow{AD}$-$\overrightarrow{BC}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com