练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知α是第三象限角，sinα=-$\frac{5}{13}$，则cosα=（　　）
    A．-$\frac{5}{13}$B．-$\frac{12}{13}$C．$\frac{5}{13}$D．$\frac{12}{13}$

    分析 由条件利用同角三角函数的基本关系，求得cosα的值．

    解答 解：∵α是第三象限角，sinα=$\frac{5}{13}$，则cosα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{12}{13}$，
    故选：B．

    点评 本题主要考查同角三角函数的基本关系，以及三角函数在各个象限中的符号，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．函数f（x）=$\frac{1}{x}$上的点到直线y=-x-1的最短距离是$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

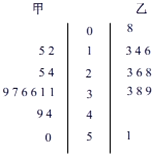    6．如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图．则甲、乙两名运动员成绩比较（　　）
    A．甲比乙稳定B．乙比甲稳定
    C．甲、乙稳定程度相同D．无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．设数列{an}的各项均为正数，它的前n项和为Sn，点（an，Sn）在函数y=$\frac{1}{8}$x2+$\frac{1}{2}$x+$\frac{1}{2}$的图象上，其中n∈N*．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设cn=$\frac{1}{{{a_n}{a_{n+1}}}}$，求数列{cn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知$\overrightarrow m$=（sinB，1-cosB），$\overrightarrow n$=（2，0），且$\overrightarrow m，\overrightarrow n$的夹角为$\frac{π}{3}$，其中A，B，C为△ABC的内角．
    （1）求角B的大小；
    （2）求sin2A+sin2C的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知等比数列{an}中，a3，a15是方程x2-6x+1=0的两根，则a7a8a9a10a11等于（　　）
    A．-1B．1C．-15D．15

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．设x＞0，y＞0，x+y≤4，则$\frac{1}{x}$+$\frac{1}{y}$的最小值为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

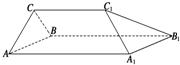    4．如图所示的几何体中，四边形AA1B1B是边长为3的正方形，CC1=2，CC1∥AA1，这个几何体是棱柱吗？若是，指出是几棱柱．若不是棱柱，请你试用一个平面截去一部分，使剩余部分是一个棱长为2的三棱柱，并指出截去的几何体的特征，在立体图中画出截面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．下列各式中不能化简为$\overrightarrow{AD}$的是（　　）
    A．$\overrightarrow{AB}$+$\overrightarrow{CD}$+$\overrightarrow{BC}$B．$\overrightarrow{AD}$+$\overrightarrow{EB}$+$\overrightarrow{BC}$+$\overrightarrow{CE}$C．$\overrightarrow{MB}$-$\overrightarrow{MA}$+$\overrightarrow{BD}$D．$\overrightarrow{CB}$+$\overrightarrow{AD}$-$\overrightarrow{BC}$

    查看答案和解析>>

    同步练习册答案