
| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-∞,-4) | D. | (-∞,-4] |
分析 直接构造基本不等式,利用基本不等式的性质即可得到答案.
解答 解:∵ab<0,
∴a,b是异号,
∴$\frac{b}{a}<0,\frac{a}{b}<0$,则$-\frac{a}{b}>0,-\frac{b}{a}>0$.
∴$\frac{b}{a}$+$\frac{a}{b}$=$-[(-\frac{a}{b})+(-\frac{b}{a})]$
由基本不等式的性质:
$(-\frac{a}{b})+(-\frac{b}{a})≥2\sqrt{(-\frac{a}{b})•(-\frac{b}{a})}=2$
∴$\frac{b}{a}$+$\frac{a}{b}$≤-2
故选B
点评 本题考查了基本不等式的性质,考查了灵活解决问题的能力,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | c<a<b | C. | b<c<a | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
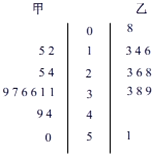 如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.则甲、乙两名运动员成绩比较( )
如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.则甲、乙两名运动员成绩比较( )| A. | 甲比乙稳定 | B. | 乙比甲稳定 | ||
| C. | 甲、乙稳定程度相同 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com