
| A. | c<a<b | B. | b<a<c | C. | a<c<b | D. | a<b<c |
分析 先由偶函数的性质求出f(x)=1-|1-x2|,由此利用对数函数和指数函数的性质能求出a,b,c的大小关系.
解答 解:∵定义在R上的函数f(x)=1-|1-(x-m)2|关于y轴对称,∴m=0,
∴f(x)=1-|1-x2|,
∵a=f(m+2)=f(2)=1-|1-22|=-2,
b=f(log5$\frac{1}{2}$)=1-|1-($lo{g}_{5}\frac{1}{2}$)2|=(log5$\frac{1}{2}$)2∈(0,1),
c=f(e${\;}^{\frac{1}{2}}}$)=1-|1-(${e}^{\frac{1}{2}}$)2|=1-|1-e|=2-e≈-0.71828,
∴a<c<b.
点评 本题考查三个数的大小关系的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
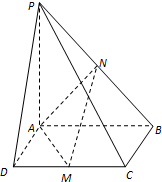 如图:已知四棱锥P-ABCD,底面是边长为6的正方形ABCD,PA=8,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.
如图:已知四棱锥P-ABCD,底面是边长为6的正方形ABCD,PA=8,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{36}$ | B. | $\frac{11}{36}$ | C. | $\frac{7}{12}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y-1)2=$\sqrt{2}$ | B. | (x+1)2+(y+1)2=$\sqrt{2}$a | C. | (x+a)2+(y+a)2=2a2 | D. | (x-a)2+(y-a)2=2a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -14 | B. | 14 | C. | -42 | D. | 42 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,4] | B. | [2,5] | C. | [2,4] | D. | [1,5] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com