Question

【题目】已知函数

（1）证明:函数在区间存在唯一的极小值点，且；

（2）证明:函数于有且仅有两个零点.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）由导数的应用，先求函数的导函数，再研究导函数的正负号即可，

因为为增函数，因为，，由零点定理运算可得存在唯一的使得，即可得证；

（2）由特值法可得是函数的一个零点，

再讨论当时，由指数函数的值域及三角函数的有界性可得函数没有零点；然后讨论时，结合（1）及零点定理可得在区间上有且仅有一个零点，在无零点，综上即可得证.

证明：（1）由.

令，

当时，函数为增函数，指数函数也为增函数，

故当时，函数为增函数.

又因为，可得，

有，

，

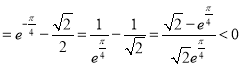故存在唯一的使得.

所以当时，，即；

当时，，即，

所以函数在区间上单调递减，在区间上单调递增，

所以函数在区间存在唯一的极小值点，且

（2）①由，可得是函数的一个零点；

②当时，，，可得，此时函数没有零点；

③当时，由，

由（1）知，，可得函数在区间上有且仅有一个零点，在无零点，

综上，函数有且仅有两个零点.