已知数列{an}的前n项和为{Sn},又有数列{bn}满足关系b1=a1,对n∈N*,有an+Sn=n,bn+1=an+1-an
(1)求证:{bn}是等比数列,并写出它的通项公式;
(2)是否存在常数c,使得数列{Sn+cn+1}为等比数列?若存在,求出c的值;若不存在,说明理由.
【答案】
分析:(1)由a
n+S
n=n,可求得2a
n+1=a
n+1,在a
n+S
n=n中令n=1可求得a
1,即b
1,由
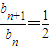
,可证明:{b
n}是等比数列,从而可得其通项公式;
(2)由可求得:a
n+b
n=a
n+a
n-a
n-1=2a
n-a
n-1,2a
n+1=a
n+1,可求得
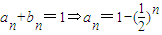
,可求得
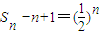
,问题即可解决.
解答:解:(1)由
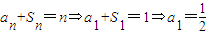
,又
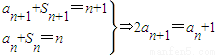
(3分)
∴
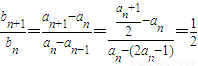
,
∴数列{b
n}为等比数列,且
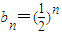
(6分)
(2)a
n+b
n=a
n+a
n-a
n-1=2a
n-a
n-1,∴
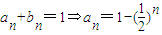
(8分)
∴
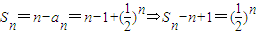
(10分)
依题意,存在c=-1,使得数列{S
n+cn+1}为等比数列. (12分)
点评:本题考查等比数列的通项公式,着重考查学生综合应用与转化的能力,属于难题.

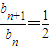 ,可证明:{bn}是等比数列,从而可得其通项公式;
,可证明:{bn}是等比数列,从而可得其通项公式;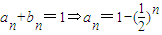 ,可求得
,可求得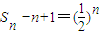 ,问题即可解决.
,问题即可解决.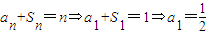 ,又
,又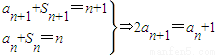 (3分)
(3分)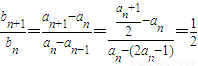 ,
,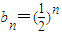 (6分)
(6分)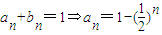 (8分)
(8分)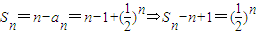 (10分)
(10分)
