解:(1)设x<0,则-x>0于是f(-x)=-2x-x
2,-------------------------
又f(x)为奇函数,所以f(x)=-f(-x)=2x+x
2,即f(x)=2x+x
2(x<0),---
(2)分下述三种情况:
①0<a<b≤1,那么

,而当x≥0,f(x)的最大值为1,
故此时不可能使g(x)=f(x),-------------------------
②若0<a<1<b,此时若g(x)=f(x),
则g(x)的最大值为g(1)=f(1)=1,得a=1,这与0<a<1<b矛盾;--------------
③若1≤a<b,因为x≥1时,f(x)是减函数,则f(x)=2x-x
2,于是有
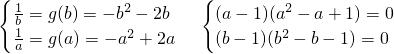
,
考虑到1≤a<b,解得
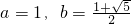
----
综上所述
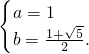
-----
分析:(1)令x<0,则-x>0,由当x≥0时,f(x)=2x-x
2,可得f(-x)的表达式,进而根据f(x)为奇函数,f(x)=-f(-x),可得答案;
(2)分0<a<b≤1,0<a<1<b和1≤a<b三种情况分别讨论,a,b的取值情况,最后综合讨论结果可得答案.
点评:本题考查的知识点是函数奇偶性的性质,函数解析式的求解及常方法,二次函数的性质,其中利用奇函数的性质,求出函数的解析式,并分析其性质是解答本题的关键.

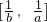 若存在,求出所有的a,b值,若不存在,请说明理由.
若存在,求出所有的a,b值,若不存在,请说明理由. ,而当x≥0,f(x)的最大值为1,
,而当x≥0,f(x)的最大值为1,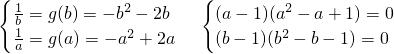 ,
,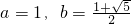 ----
---- -----
-----
