
分析 (1)根据二倍角公式及两角差的正弦公式将原式转化成lg(sinx+cosx)+lg(sinx+cosx)-lg(1+2sin2x),利用对数函数的运算性质及同角三角函数的基本关系,即可求得答案.
(2)(${x^{\frac{1}{2}}}-{x^{-\frac{1}{2}}}$)2=x+x-1-2=3-2=1,由0<x<1,${x^{\frac{1}{2}}}-{x^{-\frac{1}{2}}}$<0,即可求得${x^{\frac{1}{2}}}-{x^{-\frac{1}{2}}}$的值.
解答 解:(1)$lg(cosxtanx+1-2{sin^2}\frac{x}{2})+lg[\sqrt{2}cos(x-\frac{π}{4})]-lg(1+sin2x)$,
=lg(cosx•$\frac{sinx}{cocx}$+1-2sin2$\frac{x}{2}$)+lg($\sqrt{2}$cosxcos$\frac{π}{4}$+$\sqrt{2}$sinxsin$\frac{π}{4}$)-lg(1+2sin2x),
=lg(sinx+cosx)+lg(sinx+cosx)-lg(1+2sin2x),
=lg(sinx+cosx)2-lg(1+2sin2x),
=lg(1+2sin2x)-lg(1+2sin2x),
=0,
(2)由x+x-1=3,
(${x^{\frac{1}{2}}}-{x^{-\frac{1}{2}}}$)2=x+x-1-2=3-2=1,
由0<x<1,
∴${x^{\frac{1}{2}}}-{x^{-\frac{1}{2}}}$=$\sqrt{x}$-$\frac{1}{\sqrt{x}}$=$\frac{x-1}{\sqrt{x}}$<0,
∴${x^{\frac{1}{2}}}-{x^{-\frac{1}{2}}}$=-1
点评 本题考查三角恒等变换公式的应用,考查分数指数幂的运算法则,考查转化思想,属于中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
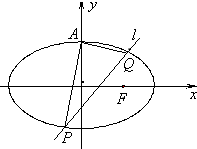 如图,已知椭圆$C:\frac{x^2}{a^2}+{y^2}=1(a>1)$的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
如图,已知椭圆$C:\frac{x^2}{a^2}+{y^2}=1(a>1)$的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com