
| A. | [2kπ+$\frac{π}{4}$,2kπ+$\frac{5π}{4}$](k∈Z) | B. | [2kπ-$\frac{3π}{4}$,2kπ+$\frac{π}{4}$](k∈Z) | ||
| C. | [2kπ-$\frac{π}{4}$,2kπ+$\frac{3π}{4}$](k∈Z) | D. | [2kπ+$\frac{3π}{4}$,2kπ+$\frac{7π}{4}$](k∈Z) |
分析 由函数f(x)=sinx+tanx是奇函数,且在($-\frac{π}{2},\frac{π}{2}$)上为增函数,把不等式f(sinθ)+f(cosθ)≥0转化为sinθ+cosθ≥0,然后求解三角不等式得答案.
解答 解:∵-1≤sinθ≤1,-1≤cosθ≤1,
而当-$\frac{π}{2}$<x<$\frac{π}{2}$时,函数f(x)=sinx+tanx是增函数,且函数f(x)=sinx+tanx是奇函数,
∴由不等式f(sinθ)+f(cosθ)≥0,得f(sinθ)≥-f(cosθ)=f(-cosθ),
即sinθ≥-cosθ,
∴sinθ+cosθ≥0,
∴sin(θ+$\frac{π}{4}$)≥0,
则2kπ≤$θ+\frac{π}{4}$≤2kπ+π,k∈Z.
解得:2kπ-$\frac{π}{4}$≤θ≤2kπ+$\frac{3π}{4}$,k∈Z.
∴使不等式f(sinθ)+f(cosθ)≥0成立的θ取值范围是[2kπ-$\frac{π}{4}$,2kπ+$\frac{3π}{4}$](k∈Z).
故选:C.
点评 本题考查三角函数的性质,考查了三角不等式的解法,体现了数学转化思想方法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | -1 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤3} | B. | {x|-1≤x<3} | C. | {-1,0,1,2,3} | D. | {-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
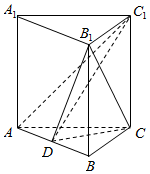 如图,在三棱柱ABC-A1B1C1中,AC=4,BC=3,AB=B1C=5,点D是线段AB的中点,四边形ACC1A1为正方形.
如图,在三棱柱ABC-A1B1C1中,AC=4,BC=3,AB=B1C=5,点D是线段AB的中点,四边形ACC1A1为正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com