
| 视觉 听觉 | 视觉记忆能力 | ||||
| 偏低 | 中等 | 偏高 | 超常 | ||
| 听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
| 中等 | 1 | 8 | 3 | b | |
| 偏高 | 2 | a | 0 | 1 | |
| 超常 | 0 | 2 | 1 | 1 | |
分析 (1)由表格数据可知,视觉记忆能力恰为中等且听觉记忆能力为中等或中等以上的学生共有(10+a)人,记“视觉记忆能力恰为中等且听觉记忆能力为中等阈 中等以上”为事件A,由等可能事件概率计算公式能求出a=6,从而得到b=2.
(2)由于从40位学生中任取3位,其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共有24人,故概率为$\frac{3}{5}$,从而ξ~B(3,$\frac{3}{5}$),由此能求出结果.
解答 解:(1)由表格数据可知,视觉记忆能力恰为中等且听觉记忆能力为中等或中等以上的学生共有(10+a)人,
记“视觉记忆能力恰为中等且听觉记忆能力为中等阈 中等以上”为事件A,
则P(A)=$\frac{10+a}{40}=\frac{2}{5}$,解得a=6,
∴b=40-(32+a)=40-38=2.
∴a=6,b=2.
(2)由于从40位学生中任取3位,其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共有24人,
故概率为$\frac{3}{5}$,
∴从该地区高二年级学生中任意抽取3人,
其中恰有k位学生具有听觉记忆能力或视觉记忆能力偏高或超常的概率P(ξ=k)=${C}_{3}^{k}(\frac{3}{5})^{k}(\frac{2}{5})^{3-k}$,(k=0,1,2,3),
ξ的可能取值为0,1,2,3,
P(ξ=0)=($\frac{2}{5}$)3=$\frac{8}{125}$,
P(ξ=1)=${C}_{3}^{1}(\frac{3}{5})(\frac{2}{5})^{2}=\frac{36}{125}$,
P(ξ=2)=${C}_{3}^{2}(\frac{3}{5})^{2}(\frac{2}{5})=\frac{54}{125}$,
P(ξ=3)=($\frac{3}{5}$)3=$\frac{27}{125}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{8}{125}$ | $\frac{36}{125}$ | $\frac{54}{125}$ | $\frac{27}{125}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是基础题,解题时要认真审题,注意二项分布的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
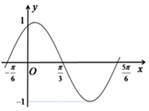 如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{6}$,$\frac{5π}{6}$]上的图象.为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上所有的点( )
如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{6}$,$\frac{5π}{6}$]上的图象.为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上所有的点( )| A. | 向左平移$\frac{π}{3}$个单位,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$倍 | |
| B. | 向左平移$\frac{π}{3}$个单位,再把所得各点的横坐标伸长到原来的2倍 | |
| C. | 向左平移$\frac{π}{6}$个单位,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$倍 | |
| D. | 向左平移$\frac{π}{6}$个单位,再把所得各点的横坐标伸长到原来的2倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
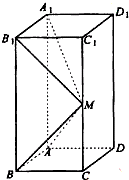 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com