解:(1)∵f(0)=b,∴点P (0,b).∵f′(x)=x
2-2x+a,
∴函数f(x)的图象在点P处的切线斜率为 a,故此处的切线方程为 y-b=a (x-0),
即 y=ax+b.又已知此处的切线方程为y=3x-2,∴a=3,b=-2.
(2)∵h(x)=f(x)-6x=

x
3-x
2+ax+b-6x=

x
3-x
2 -3x-2,
∴h′(x)=x
2-2x-3,令 h′(x)=0,得 x=-1,或 x=3.
在x=-1的左侧,h′(x)>0,在x=-1的右侧,h′(x)<0,故h(x)在x=-1处取极大值为-

.
在x=3 的左侧,h′(x)<0,在x=3的右侧,h′(x)>0,故h(x)在x=-1处取极小值为-11.
(3)∵k(x)=f(x)+
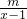
=

x
3-x
2+3x-2+
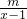
,k′(x)=
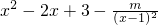
.
由题意得,k′(x)在[2,+∞)上 大于或等于0,即 x≥2时,
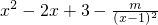
≥0 恒成立,
即 m≤(x
2-2x+3 )(x-1)
2 恒成立.
∵(x
2-2x+3 )(x-1)
2 在[2,+∞)上是单调增函数,故x≥2时(x
2-2x+3 )(x-1)
2 的最小值为3,
∴m≤3.
分析:(1)利用导数的几何意义求出切线的斜率,点斜式求得切线方程,和已知的切线方程比较系数可得a、b值.
(2)求出 h′(x),利用h′(x)研究h(x)的单调性,由单调性求出h(x)的极值.
(3)化简k(x)=f(x)+
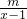
的解析式,由题意得x≥2时,导数k′(x)≥0 恒成立,即x≥2时,m≤(x
2-2x+3)(x-1)
2 恒成立,故m 小于或等于(x
2-2x+3 )(x-1)
2 的最小值3.
点评:本题考查导数的几何意义,利用导数研究函数的单调性和极值,求出x≥2时(x
2-2x+3 )(x-1)
2 的最小值是
解题的难点.

 x3-x2+ax+b的图象在点P(0,f(0))处的切线方程为y=3x-2.
x3-x2+ax+b的图象在点P(0,f(0))处的切线方程为y=3x-2.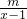 是[2,+∞)上的增函数,求实数m的取值范围.
是[2,+∞)上的增函数,求实数m的取值范围. x3-x2+ax+b-6x=
x3-x2+ax+b-6x= x3-x2 -3x-2,
x3-x2 -3x-2, .
.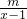 =
= x3-x2+3x-2+
x3-x2+3x-2+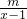 ,k′(x)=
,k′(x)=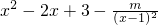 .
.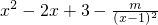 ≥0 恒成立,
≥0 恒成立,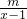 的解析式,由题意得x≥2时,导数k′(x)≥0 恒成立,即x≥2时,m≤(x2-2x+3)(x-1)2 恒成立,故m 小于或等于(x2-2x+3 )(x-1)2 的最小值3.
的解析式,由题意得x≥2时,导数k′(x)≥0 恒成立,即x≥2时,m≤(x2-2x+3)(x-1)2 恒成立,故m 小于或等于(x2-2x+3 )(x-1)2 的最小值3.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<