
【题目】已知![]() 是等差数列,
是等差数列, ![]() 是等比数列,
是等比数列, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() 的通项公式;
的通项公式;
(2)![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)根据![]() 是等差数列,
是等差数列, ![]() 是等比数列,
是等比数列, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 列出关于公比
列出关于公比![]() 、公差
、公差![]() 的方程组,解方程组可得
的方程组,解方程组可得![]() 与
与![]() 的值,从而可得数列
的值,从而可得数列![]() ,
, ![]() 的通项公式;(2)由(1)可知
的通项公式;(2)由(1)可知![]() ,根据错位相减法结合等比数列的求和公式可得
,根据错位相减法结合等比数列的求和公式可得![]() 的前
的前![]() 项和为
项和为![]() ,利用放缩法可得结论.
,利用放缩法可得结论.
试题解析:(1)设![]() 公差为
公差为![]() ,
, ![]() 公比为
公比为![]() ,
,
由题意得:  ,
,
解得![]() ,或
,或![]() (舍),
(舍),
∴![]() ,
, ![]() .
.
(2)![]()
![]() ,
,
![]()
![]() ,
,
相减得: ![]()
![]()
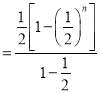
![]() ,
,
∴![]() ,∴
,∴![]() .
.
【 方法点睛】本题主要考查等比数列和等差数列的通项以及错位相减法求数列的前![]() 项和,属于中档题.一般地,如果数列
项和,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列, ![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”与“
”与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,矩形ADEF与梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,M为CE的中点,N为CD中点.
,M为CE的中点,N为CD中点.
![]() 求证:平面
求证:平面![]() 平面ADEF;
平面ADEF;
![]() 求证:平面
求证:平面![]() 平面BDE;
平面BDE;
![]() 求点D到平面BEC的距离.
求点D到平面BEC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,△PBC为正三角形,AB⊥平面PBC,AB∥CD,AB=![]() DC,
DC, ![]() .
.
(1)求证:AE∥平面PBC;
(2)求证:AE⊥平面PDC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,B、E、F为山脚两侧共线的三点,在山顶A处测得这三点的俯角分别为![]() 、
、![]() 、
、![]() ,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.

(1)求出线段AE的长度;
(2)求出隧道CD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}为递增的等差数列,数列{bn}满足bn=anan+1an+2(n∈N*),设Sn为数列{bn}的前n项和,若a2![]() ,则当Sn取得最小值时n的值为( )
,则当Sn取得最小值时n的值为( )
A.14B.13C.12D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现安排甲、乙、丙、丁、戊5名同学参加2022年杭州亚运会志愿者服务活动,有翻译、导游、礼仪、司机四项工作可以安排,以下说法正确的是( )
A. 每人都安排一项工作的不同方法数为![]()
B. 每项工作至少有一人参加,则不同的方法数为![]()
C. 如果司机工作不安排,其余三项工作至少安排一人,则这5名同学全部被安排的不同方法数为![]()
D. 每项工作至少有一人参加,甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
(1) 已知![]() ,
,![]() ,
,![]() ,则
,则![]()
(2)将6个相同的小球放入4个不同的盒子中,要求不出现空盒,共有10种放法.
(3) ![]() 被
被![]() 除后的余数为
除后的余数为![]() .
.
(4) 若![]() ,则
,则![]() =
=![]()
(5)抛掷两个骰子,取其中一个的点数为点![]() 的横坐标,另一个的点数为点
的横坐标,另一个的点数为点![]() 的纵坐标,连续抛掷这两个骰子三次,点
的纵坐标,连续抛掷这两个骰子三次,点![]() 在圆
在圆![]() 内的次数
内的次数![]() 的均值为
的均值为![]()
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若命题![]() 都是真命题,则命题“
都是真命题,则命题“![]() ”为真命题
”为真命题
B. 命题“![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C. 命题:“若![]() ,则
,则![]() 或
或![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() 或
或![]() ”
”
D. “![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)令![]() ,试讨论
,试讨论![]() 的单调性;
的单调性;
(2)若对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由![]() ,对函数求导,研究导函数的正负得到单调性即可;(2)由条件可知
,对函数求导,研究导函数的正负得到单调性即可;(2)由条件可知![]() 对
对![]() 恒成立,变量分离
恒成立,变量分离![]() ,令
,令![]() ,求这个函数的最值即可.
,求这个函数的最值即可.
解析:
(1)由![]() 得
得![]()
当![]() 时,
时, ![]() 恒成立,则
恒成立,则![]() 单调递减;
单调递减;
当![]() 时,
时,  ,令
,令 ,
,
令 .
.
综上:当![]() 时,
时, ![]() 单调递减,无增区间;
单调递减,无增区间;
当![]() 时,
时,  ,
, 
(2)由条件可知![]() 对
对![]() 恒成立,则
恒成立,则
当![]() 时,
时, ![]() 对
对![]() 恒成立
恒成立
当![]() 时,由
时,由![]() 得
得![]() .令
.令![]() 则
则
 ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]()
所以![]() ,从而可知
,从而可知![]() .
.
综上所述: 所求![]() .
.
点睛:导数问题经常会遇见恒成立的问题:
(1)根据参变分离,转化为不含参数的函数的最值问题;
(2)若 ![]() 就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为
就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为![]() ,若
,若![]() 恒成立
恒成立![]() ;
;
(3)若![]() 恒成立,可转化为
恒成立,可转化为![]() (需在同一处取得最值) .
(需在同一处取得最值) .
【题型】解答题
【结束】
22
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴的极坐标系中,直线
轴的非负半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com