练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设抛物线x2＝－2py(p＞0)的焦点为F，准线为l，A(x1，y1)，B(x2，y2)是抛物线上不同两点，且与为共线向量．

    (1)求证：x1·x2＝－p2

    (2)l上是否存在点C，使·＝0，试证明你的结论．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    设函数y＝f(x)的图象为抛物线，并且当点(x，y)在f(x)的图象上任意移动时，点(x，y2＋1)在函数y＝g(x)＝f[f(x)]的图象上移动，求g(x)的表过式．

    查看答案和解析>>

    科目：高中数学 来源：2007届深圳市龙华中英文实验学校理科数学测试题 题型：044

    解答题：解答应写出文字说明，证明过程或演算步骤

    如图，过抛物线x2＝4y的对称轴上任一点P(0，m)(m＞0)作直线与抛物线交于A、B两点，点Q是点P关于原点的对称点．

    (1)

    设点P分有向线段所成的比为λ，证明

    (2)

    设直线AB的方程是x—2y＋12＝0，过A、B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程．

    查看答案和解析>>

    科目：高中数学 来源：汕头市2007年普通高校招生模拟考试(二)、理科数学 题型：044

    解答题：解答应写出文字说明，证明过程或演算步骤．

    设P(x1，y1)，Q(x2，y2)是抛物线C：y2＝2px(p＞0)上相异两点，且，直线PQ与x轴相交于E．

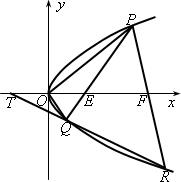
    (Ⅰ)若P，Q到x轴的距离的积为4，求p的值；

    (Ⅱ)若p为已知常数，在x轴上，是否存在异于E的一点F，使得直线PF与抛物线的另一交点为R，而直线RQ与x轴相交于T，且有，若存在，求出F点的坐标(用p表示)，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：陕西部分学校2008年5月高三联合测试、文科数学测题 题型：044

    解答题(解答写出文字说明，证明过程)

    抛物线C的方程为y＝ax2(a＜0)，过抛物线C上一点P(x0，y0)(x0≠0)作斜率为k1，k2的两条直线交抛物线于A(x1，y1)，B(x2，y2)两点，(P、A、B三点互不相同)，且满足k2＋λk1＝0(x0≠0，且λ≠－1)．

    (1)设直线AB上一点M，满足证明线段PM的中点在y轴上．

    (2)当λ＝1时，若点p的坐标为(1，－1)，求∠PAB为钝角时，A的纵坐标y1的取值范围．

    查看答案和解析>>

    同步练习册答案