
| 2 |
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
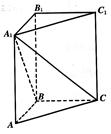
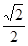 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
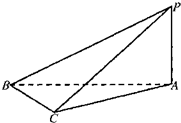
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 2 |
| A.A'C⊥BD | ||
| B.∠BA'C=90° | ||
| C.△A'DC是正三角形 | ||
D.四面体A'-BCD的体积为
|
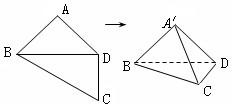
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
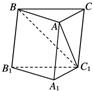
| A.直线AB上 | B.直线BC上 | C.直线CA上 | D.△ABC内部 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(-4,-8,6) | B.(-4,8,-6) | C.(4,-8,-6) | D.(4,-8,6) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,对函数
,对函数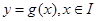 ,定义
,定义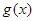 关于
关于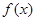 的对称函数为函数
的对称函数为函数 ,
,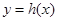 满足:对于任意
满足:对于任意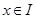 ,两个点
,两个点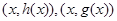 关于点
关于点 对称,若
对称,若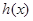 是
是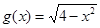 关于
关于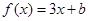 的“对称函数”,且
的“对称函数”,且 恒成立,则实数
恒成立,则实数 的取值范围是_________.
的取值范围是_________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com