设数列{an}的前n项和为Sn,且满足Sn=n-an,n∈N*.
(Ⅰ)证明数列{an-1}是等比数列;
(Ⅱ)设cn=-2nan+2n,数列{cn}的前n项和为Tn,求证:Tn<4.
解:(Ⅰ)∵n=1时,S
1=1-a
1,即a
1=1-a
1,a
1=

.
∵S
n=n-a
n,∴S
n-1=n-1-a
n-1,n>1.
两式相减,得a
n=

a
n-1+

.…(3分)
a
n-1=

(a
n-1-1).
从而{a
n-1}为等比数列,首项a
1-1=-

,公比为

.…(6分)
(Ⅱ)由(Ⅰ)知a
n-1=
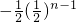
.从而a
n=
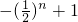
.…(8分)
∵c
n=-2na
n+2n,∴
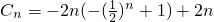
=
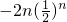
,
∴
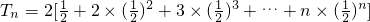
.…(10分)
从而
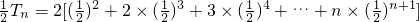
,
两式相减,得
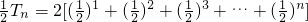
.
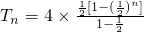
-
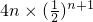
=
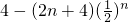
.
∴T
n<4.…(13分)
分析:(Ⅰ)求出a
1,然后利用a
n=S
n-S
n-1得到a
n与a
n-1的关系,化简为数列{a
n-1}中任意相邻两项之间的关系,通过等比数列的定义证明数列是等比数列;
(Ⅱ)通过(Ⅰ)求出数列的通项公式,结合c
n=-2na
n+2n,求出数列{c
n}的前n项和为T
n的表达式,利用错位相减法求出数列的前n项和,即可求证:T
n<4.
点评:证明数列是等差数列还是等比数列,常用数列的定义证明,在第二问中,错位相减法是数列求和的常用方法,注意构造法在数列中的应用.

 .
. an-1+
an-1+ .…(3分)
.…(3分) (an-1-1).
(an-1-1). ,公比为
,公比为 .…(6分)
.…(6分)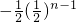 .从而an=
.从而an=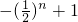 .…(8分)
.…(8分)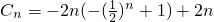 =
=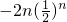 ,
,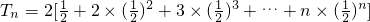 .…(10分)
.…(10分)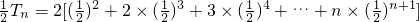 ,
,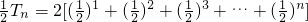 .
.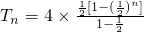 -
-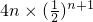 =
=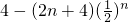 .
.

 应用题作业本系列答案
应用题作业本系列答案