
【题目】已知定点![]() 和直线
和直线![]() 上的动点
上的动点![]() ,线段
,线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(I)求曲线![]() 的方程;
的方程;
(II)直线![]() 交
交![]() 轴于点
轴于点![]() ,交曲线
,交曲线![]() 于不同的两点
于不同的两点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求证:
,求证:![]() 三点共线.
三点共线.
【答案】(I)![]() ;(II)证明见解析.
;(II)证明见解析.
【解析】
试题分析:(I)根据题意分析可知,动点![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() 的距离相等,因此动点
的距离相等,因此动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,以直线
为焦点,以直线![]() 为准线的抛物线,轨迹方程
为准线的抛物线,轨迹方程![]() ;(II)联立直线方程与抛物线方程
;(II)联立直线方程与抛物线方程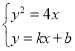 ,消去
,消去![]() 得:
得:![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,![]() ,点
,点![]() ,由
,由![]() 知
知![]() ,则
,则![]() ,若
,若![]() 三点共线,则应有
三点共线,则应有![]() ,即验证
,即验证![]() 即可.
即可.
试题解析:(I)由题意可知:![]() ,即点
,即点![]() 到直线
到直线![]() 和点
和点![]() 的距离相等,根据抛物线的定义可知:
的距离相等,根据抛物线的定义可知:![]() 的轨迹为抛物线,其中
的轨迹为抛物线,其中![]() 为焦点. ……………………………3分
为焦点. ……………………………3分
设![]() 的轨迹方程为:
的轨迹方程为:![]()
所以![]() 的轨迹方程为:
的轨迹方程为:![]() . ……………………………5分
. ……………………………5分
(II)由条件可知![]() ,则
,则![]() . ……………………………6分
. ……………………………6分
联立 ,消去
,消去![]() 得
得![]() ,
,
![]() . …………………………… 7分
. …………………………… 7分
设![]() ,则
,则![]()
![]()
![]() …………………………… 9分
…………………………… 9分
因为 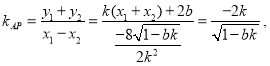 …………………………… 10分
…………………………… 10分
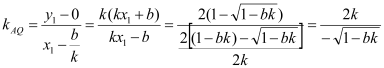 …………………………… 11分
…………………………… 11分
所以![]() 三点共线. …………………………… 12分
三点共线. …………………………… 12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
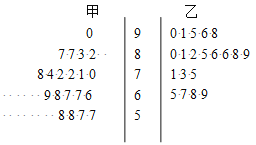
(1)学校规定:成绩不低于75分的为优秀.请画出下面的![]() 列联表.
列联表.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(2)判断有多大把握认为“成绩优秀与教学方式有关”.
下面临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数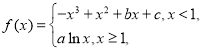 图象过点
图象过点![]() ,且在该点处的切线与直线
,且在该点处的切线与直线![]() 垂直.
垂直.
(1)求实数![]() ,
,![]() 的值;
的值;
(2)对任意给定的正实数![]() ,曲线
,曲线![]() 上是否存在两点
上是否存在两点![]() ,
,![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在![]() 轴上?
轴上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长均相等的正三棱柱ABCA1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:
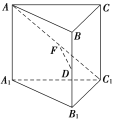
①AC1⊥BC;
②AF=FC1;
③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上有两个不同的零点,求实数
上有两个不同的零点,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,请求出最大整数
的图象的下方?若存在,请求出最大整数![]() 的值;若不存在,请说理由.
的值;若不存在,请说理由.
(参考数据: ![]() ,
, ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com