
【题目】莫言是中国首位获得诺贝尔文学奖的文学家,国人欢欣鼓舞。某高校文学社从男女生中各抽取50名同学调查对莫言作品的了程度,结果如下:
阅读过莫言的作品数(篇) | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
男生 | 3 | 6 | 11 | 18 | 12 |
女生 | 4 | 8 | 13 | 15 | 10 |
(1)试估计该学校学生阅读莫言作品超过50篇的概率.
(2)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”,根据题意完成下表,并判断能否有![]() 的把握认为“对莫言作品的非常了解”与性别有关?
的把握认为“对莫言作品的非常了解”与性别有关?
非常了解 | 一般了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
注:K2=
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点
的图象经过点![]() ,对任意实数
,对任意实数![]() 满足
满足![]() ,且函数
,且函数![]() 的最小值为2.
的最小值为2.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,其中
,其中![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值
上的最小值![]() ;
;
(3)若在区间![]() 上,函数
上,函数![]() 的图象恒在函数
的图象恒在函数![]() 的图象上方,试确定实数
的图象上方,试确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
专业A | 专业B | 总计 | |
女生 | 12 | 4 | 16 |
男生 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
(1)从B专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(2)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢?
注:K2=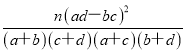
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是正方体ABCD-A1B1C1D1中BC1上的动点,下列说法:

①AP⊥B1C;②BP与CD1所成的角是60°;③三棱锥![]() 的体积为定值;④B1P∥平面D1AC;⑤二面角P-AB-C的平面角为45°.
的体积为定值;④B1P∥平面D1AC;⑤二面角P-AB-C的平面角为45°.
其中正确说法的个数有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O![]() 的直径,FB是圆台的一条母线.
的直径,FB是圆台的一条母线.
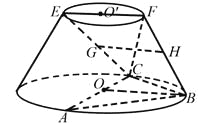
(Ⅰ)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB=![]() AC=
AC=![]() ,AB=BC.求二面角
,AB=BC.求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解校园安全教育系列活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
等级 | 不及格 | 及格 | 良好 | 优秀 |
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
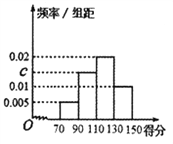
(1)求![]() 的值;
的值;
(2)试估计该校安全意识测试评定为“优秀”的学生人数;
(3)已知已采用分层抽样的方法,从评定等级为“优秀”和“良好”的学生中任选6人进行强化培训;现再从这6人中任选2人参加市级校园安全知识竞赛,求选取的2人中有1人为“优秀”的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,且x=-1处取得极大 值2.
为奇函数,且x=-1处取得极大 值2.
(1)求f(x)的解析式;
(2)过点A(1,t) ![]() 可作函数f(x)图像的三条切线,求实数t的取值范围;
可作函数f(x)图像的三条切线,求实数t的取值范围;
(3)若![]() 对于任意的
对于任意的![]() 恒成立,求实数m取值范围.
恒成立,求实数m取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com