
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O![]() 的直径,FB是圆台的一条母线.
的直径,FB是圆台的一条母线.
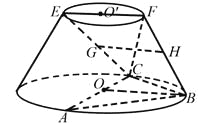
(Ⅰ)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB=![]() AC=
AC=![]() ,AB=BC.求二面角
,AB=BC.求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]()
【解析】试题分析:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() ,推导出平面
,推导出平面![]() 平面
平面![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;(Ⅱ)由
;(Ⅱ)由![]() ,知
,知![]() ,以
,以![]() 为原点,
为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法能求出二面角
轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
试题解析:(Ⅰ)连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() 、
、![]() 在上底面内,
在上底面内, ![]() 不在上底面内,
不在上底面内, ![]() 上底面,………………2分
上底面,………………2分
![]() 平面
平面![]() ,又
,又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,………………4分
,………………4分
所以平面![]() 平面
平面![]() ,由
,由![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .………………5分
.………………5分
(Ⅱ)连结![]() ,
, ![]() ,
, ![]() ,………………6分
,………………6分
以![]() 为原点,分别以
为原点,分别以![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() ,
, ![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
![]() ,
, ![]() ,
, ![]() ,
,
于是有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
可得平面![]() 中的向量
中的向量![]() ,
, ![]() ,于是得平面
,于是得平面![]() 的一个法向量
的一个法向量![]() ,………………9分
,………………9分
又平面![]() 的一个法向量
的一个法向量![]() ………………10分
………………10分
设二面角![]() 为
为![]() ,则
,则 ,
,
二面角![]() 的余弦值为
的余弦值为![]() ………………12分
………………12分


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 与
与![]() 的两个交点间的距离为
的两个交点间的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)分别过![]() 作
作![]() 满足
满足![]() ,设
,设![]() 与
与![]() 的上半部分分别交于
的上半部分分别交于![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求方程![]() 的实数解;
的实数解;
(Ⅱ)如果数列![]() 满足
满足![]() ,
,![]() (
(![]() ),是否存在实数
),是否存在实数![]() ,使得
,使得![]() 对所有的
对所有的![]() 都成立?证明你的结论.
都成立?证明你的结论.
(Ⅲ)在(Ⅱ)的条件下,设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】莫言是中国首位获得诺贝尔文学奖的文学家,国人欢欣鼓舞。某高校文学社从男女生中各抽取50名同学调查对莫言作品的了程度,结果如下:
阅读过莫言的作品数(篇) | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
男生 | 3 | 6 | 11 | 18 | 12 |
女生 | 4 | 8 | 13 | 15 | 10 |
(1)试估计该学校学生阅读莫言作品超过50篇的概率.
(2)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”,根据题意完成下表,并判断能否有![]() 的把握认为“对莫言作品的非常了解”与性别有关?
的把握认为“对莫言作品的非常了解”与性别有关?
非常了解 | 一般了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
注:K2=
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
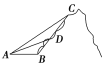
【题目】如图,嵩山上原有一条笔直的山路BC,现在又新架设了一条索道AC,小李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登400米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登800米方到达C处,则索道AC的长为________米.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
年份200 | 0 | 1 | 2 | 3 | 4 |
人口数 | 5 | 7 | 8 | 11 | 19 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)据此估计2005年该城市人口总数.
参考公式: 用最小二乘法求线性回归方程系数公式 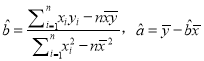
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个圆柱形乒乓球筒,高为![]() 厘米,底面半径为
厘米,底面半径为![]() 厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com