
分析 根据题意,由函数单调性的性质,可得$\left\{\begin{array}{l}{-\frac{2m}{2×(-1)}≥1}\\{2m-3≤1}\end{array}\right.$,解可得m的取值范围,即可得答案.
解答 解:根据题意,函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2mx-2,x<1}\\{1+lnx,x≥1}\end{array}\right.$是(-∞,+∞)上的增函数,
则必有$\left\{\begin{array}{l}{-\frac{2m}{2×(-1)}≥1}\\{2m-3≤1}\end{array}\right.$,
解可得1≤m≤2;
即m的取值范围是[1,2];
故答案为:[1,2].
点评 本题考查函数单调性的性质,关键是充分利用函数的单调性得到关于m的不等式组.


科目:高中数学 来源: 题型:解答题
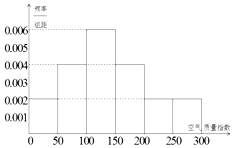 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+2ln2}{4}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:选择题
幂函数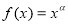 的图象经过点(2,4),则
的图象经过点(2,4),则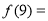 ( )
( )
A.1 B.3 C.9 D.81
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{e}$) | B. | (2$\sqrt{2}$,+∞) | C. | (e+$\frac{2}{e}$,+∞) | D. | ($\frac{{e}^{2}}{2}$+$\frac{4}{{e}^{2}}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com