练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知点A（3，5）及直线l：x-2y+2=0，B为y轴上的动点，C为l上的动点，则△ABC的周长的最小值为4$\sqrt{5}$．．

    分析 A关于y轴的对称点M，A关于l：x-2y+2=0的对称点D，连接MD交直线l：x-2y+2=0与C，交y轴于B，则此时△ABC的周长的值最小，求出DM即可．

    解答 解：A关于y轴的对称点M，A关于l：x-2y+2=0的对称点D，
    ∴MB=BA，AC=CD
    连接MD交直线l：x-2y+2=0与C，交y轴于B，
    则此时△ABC的周长的值最小，即DM的长度即为三角形周长的最小值，
    由题意及作图知M（-3，5）．D（5，1）
    由两点距离公式知，DM=$\sqrt{（5+3）^{2}+（1-5）^{2}}$=4$\sqrt{5}$．
    故答案为4$\sqrt{5}$．

    点评 考查学生会利用对称求线段最小长度，以及两点间距离公式的应用能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=$\sqrt{3}$sinxcosx-cos2x-$\frac{1}{2}$．
    （1）求函数y=f（x）在x∈[0，$\frac{π}{2}}$]时的值域；
    （2）在△ABC中，角A、B、C所对的边分别为a、b、c，且满足c=2，a=3，f（B）=0，求边b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．设函数f（x）=$\left\{\begin{array}{l}m+{x^2}\;\;，\;\;|x|≥1\\ x\;\;\;，\;\;\;\;|x|＜1\end{array}$的图象过点（1，1），函数g（x）是二次函数，若函数f（g（x））的值域是[0，+∞），则函数g（x）的值域是（　　）
    A．（-∞，1]∪[1，+∞）B．（-∞，-1]∪[0，+∞）C．[0，+∞）D．[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知△ABC中，$\frac{c-b}{c-a}$=$\frac{sinA}{sinC+sinB}$，则B=（　　）
    A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{3π}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知a，b，c∈R，对于任意的实数x，均有|ax2+bx+c|≥|x2-3x+2|．求|b2-4ac|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知lga、lgb是一元二次方程x2-3x+1=0的两个根，且1ga＞lgb，求$\frac{a}{b}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=|2x-1|+|2x+1|
    （Ⅰ）画出y=f（x）的图象；
    （Ⅱ）判断f（x）的奇偶性
    （Ⅲ）根据图象填空：求f（x）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

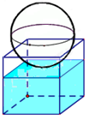    4．如图是一个水平放置的透明无盖的正方体容器，高12cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为8cm，如果不计容器的厚度，则球的体积为（　　）
    A．$\frac{169π}{6}$cm3B．$\frac{676π}{3}$cm3C．$\frac{8788π}{3}$cm3D．$\frac{2197π}{6}$cm3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知菱形ABCD的两个顶点坐标：A（-2，1），C（0，5），则对角线BD所在直线方程为（　　）
    A．x+2y-5=0B．2x+y-5=0C．x-2y+5=0D．2x-y+5=0

    查看答案和解析>>

    同步练习册答案