练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．在空间，下列条件可以确定一个平面的是（　　）
    A．两条直线B．一点和一条直线C．一个三角形D．三个点

    分析 在A中，两条异面直线不能确定一个平面；在B中，若点在直线上，由不能确定一个平面；在C中，一个三角形确定一个平面；在D中，如果共点共线，不能确定一个平面．

    解答 解：在A中，两条相交线和两条平行线都能确定一个平面，
    但两条异面直线不能确定一个平面，故A错误；
    在B中，直线与直线外一点确定一个平面，
    若点在直线上，由不能确定一个平面，故B错误；
    在C中，因为一个三角形的三个顶点不共线，所以一个三角形确定一个平面，故C正确；
    在D中，不共线的三点确定一个平面，如果共点共线，不能确定一个平面，故D错误．
    故选：C．

    点评 本题考查能确定一个平面的充要条件的判断，是基础题，解题时要认真审题，注意平面的基本性质及推论的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．已知等差数列{an}中，a2，a8是函数f（x）=x2-3x+5的两个零点．则a1+a9的值为（　　）
    A．-3B．5C．3D．-5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知数列1，a1，a2，4成等差数列，1，b1，b2，b3，4成等比数列，则$\frac{b_2}{{{a_2}-{a_1}}}$=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．点（1，-2）到直线x-y=1的距离为$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．在平面直角坐标系xOy中，圆C：（x-1）2+y2=5和y轴的负半轴相交于A点，点B在圆C上（不同于点A），M为AB的中点，且|OA|=|OM|，则点M的坐标为$（\frac{8}{5}，-\frac{6}{5}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

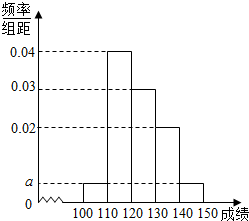    16．贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示，其中成绩分组区间是[100，110），[110，120），[120，130），[130，140），[140，150]．
    （Ⅰ）求图中a的值；
    （Ⅱ）根据频率分布直方图，估计这100名学生数学成绩的平均分；
    （Ⅲ）若这100名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如下表所示，求语文成绩在[100，140）之外的人数．
    分数段[100，110）[110，120）[120，130）[130，140）
    x：y1：12：13：44：5

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．函数$f（x）=sin（x+\frac{π}{6}）cos（x+\frac{π}{6}）$，给出下列结论正确的是（　　）
    A．f（x）的最小正周期为 $\frac{π}{2}$B．f（x）的一条对称轴为$x=\frac{π}{6}$
    C．f（x）的一个对称中心为$（\frac{π}{6}，0）$D．$f（x-\frac{π}{6}）$是奇函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．函数f（x）=1+log2（-x）与g（x）=2x-1在同一直角坐标系下的图象大致是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知sin（π+θ）=$\frac{1}{2}$，求$\frac{cos（3π+θ）}{cos[cos（π-θ）-1]}$+$\frac{cos（θ-2π）}{sin（θ-\frac{7π}{2}）cos（π-θ）-sin（\frac{3π}{2}+θ）}$的值．

    查看答案和解析>>

    同步练习册答案