
分析 (1)根据奇函数的定义即可证明,
(2)根据单调性的定义即可证明;
(3)由(1)(2)得f(x)在[-2,-3]上单调递增,即可求出最值.
解答 解:(1)证明:$f(-x)=\frac{{{{(-x)}^2}+1}}{-x}=\frac{{{x^2}+1}}{-x}=-f(x)$
故f(x)为奇函数---------------------------------(3分)
(2)在[1,+∞)上任取x1<x2,则$f({x_1})-f({x_2})=\frac{{{x_1}^2+1}}{x_1}-\frac{{{x_2}^2+1}}{x_2}=\frac{{({x_1}-{x_2})({x_1}{x_2}-1)}}{{{x_1}{x_2}}}$
因为1<x1<x2<+∞,所以x1x2>1,x1-x2<0
故$\frac{{({x_1}-{x_2})({x_1}{x_2}-1)}}{{{x_1}{x_2}}}<0$
所以f(x1)<f(x2),所以f(x)在[1,+∞)上单调递增.----------------(8分)
(3)由(1)(2)得f(x)在[-2,-3]上单调递增.
所以$f{(x)_{max}}=f(-3)=-\frac{10}{3}$,$f{(x)_{min}}=f(-2)=-\frac{5}{2}$----------------(12分)
点评 本题考查了函数的奇偶性和单调性的证明以及单调性的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
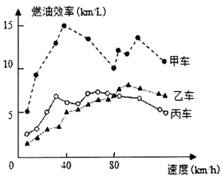 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )| A. | 消耗1升汽油,乙车最多可行驶5千米 | |
| B. | 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多 | |
| C. | 某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油 | |
| D. | 甲车以80千米/小时的速度行驶1小时,消耗10升汽油 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<1} | B. | {x|-1≤x<2} | C. | {x|1≤x<2} | D. | {x|-1≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com