
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点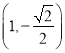 是椭圆
是椭圆![]() 上的点,离心率
上的点,离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 在椭圆
在椭圆![]() 上,若点
上,若点![]() 与点
与点![]() 关于原点对称,连接
关于原点对称,连接![]() 并延长与椭圆
并延长与椭圆![]() 的另一个交点为
的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据条件列出关于![]() 两个方程,解方程组可得
两个方程,解方程组可得![]() 值,即得椭圆
值,即得椭圆![]() 的方程;(2)联立直线方程与椭圆方程,利用韦达定理及弦长公式可得底边长
的方程;(2)联立直线方程与椭圆方程,利用韦达定理及弦长公式可得底边长![]() (用直线斜率表示),根据点到直线距离公式可得三角形的高(用直线斜率表示),根据三角形面积公式可得
(用直线斜率表示),根据点到直线距离公式可得三角形的高(用直线斜率表示),根据三角形面积公式可得![]() 面积,关于直线斜率的函数关系式,最后根据分式函数求值域方法求函数最值,注意讨论斜率不存在的情形.
面积,关于直线斜率的函数关系式,最后根据分式函数求值域方法求函数最值,注意讨论斜率不存在的情形.
试题解析:(1)依题意,![]() ,
,![]() ,
,![]() ,解得
,解得![]() 。
。
故椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 的斜率不存在时,不妨取
的斜率不存在时,不妨取![]() ,
,
故![]() .
.
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
联立方程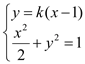 化简得
化简得![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
因为![]() 是线段
是线段![]() 的中点,所以点
的中点,所以点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴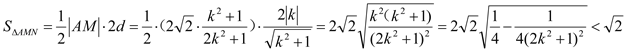 .
.
综上,![]() 面积的最大值为
面积的最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}是一个公差大于0的等差数列,且满足![]() ,a2+a7=16
,a2+a7=16
(1)求数列{an}的通项公式;
(2)数列{an}和数列{bn}满足等式![]() (n∈N*),求数列{bn}的前n项和Sn.
(n∈N*),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为![]() 的圆形纸板内有一个相同圆心的半径为
的圆形纸板内有一个相同圆心的半径为![]() 的小圆,现将半径为
的小圆,现将半径为![]() 的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ![]() =
= 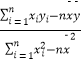 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,
,
参考数据:7×165+6×142+6×148+5×125+6×150=4420.
查看答案和解析>>
科目:高中数学 来源: 题型:
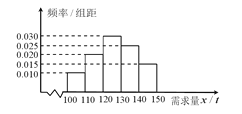
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的空间几何体中,底面四边形![]() 为正方形,
为正方形, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
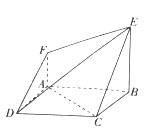
(1)求二面角![]() 的大小;
的大小;
(2)若在平面![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,试通过计算说明点
,试通过计算说明点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知 ![]() tanAtanB﹣tanA﹣tanB=
tanAtanB﹣tanA﹣tanB= ![]() .
.
(1)求∠C的大小;
(2)设角A,B,C的对边依次为a,b,c,若c=2,且△ABC是锐角三角形,求a2+b2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【广东省惠州市2017届高三上学期第二次调研】已知点![]() ,点
,点![]() 是圆
是圆![]()
![]() 上的任意一点,线段
上的任意一点,线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交于点
交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)若直线![]() 与点
与点![]() 的轨迹有两个不同的交点
的轨迹有两个不同的交点![]() 和
和![]() ,且原点
,且原点![]() 总在以
总在以![]() 为直径的圆的内部,求实数
为直径的圆的内部,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2, ![]() .M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点. 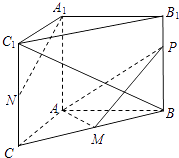
(1)求证:平面APM⊥平面BB1C1C;
(2)若P为线段BB1的中点,求证:A1N∥平面APM;
(3)试判断直线BC1与平面APM是否能够垂直.若能垂直,求PB的值;若不能垂直,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com