
【题目】在△ABC中,已知 ![]() tanAtanB﹣tanA﹣tanB=
tanAtanB﹣tanA﹣tanB= ![]() .
.
(1)求∠C的大小;
(2)设角A,B,C的对边依次为a,b,c,若c=2,且△ABC是锐角三角形,求a2+b2的取值范围.
【答案】
(1)解:依题意: ![]() ,即
,即 ![]() .
.
又0<A+B<π,∴ ![]() ,
,
∴ ![]()
(2)解:由三角形是锐角三角形可得 ![]() ,
, ![]() 即
即 ![]() .
.
由正弦定理得 ![]() ,
,
∴ ![]()
![]()
= ![]()
![]()
= ![]() .
.
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,从而
,从而 ![]() .
.
则a2+b2的取值范围为:( ![]() ,8]
,8]
【解析】(1)由已知中 ![]() tanAtanB﹣tanA﹣tanB=
tanAtanB﹣tanA﹣tanB= ![]() ,变形可得
,变形可得 ![]() ,由两角和的正切公式,我们易得到A+B的值,进而求出∠C的大小;(2)由c=2,且△ABC是锐角三角形,再由正弦定理,我们可以将a2+b2转化为一个只含A的三角函数式,根据正弦型函数的性质,我们易求出a2+b2的取值范围.
,由两角和的正切公式,我们易得到A+B的值,进而求出∠C的大小;(2)由c=2,且△ABC是锐角三角形,再由正弦定理,我们可以将a2+b2转化为一个只含A的三角函数式,根据正弦型函数的性质,我们易求出a2+b2的取值范围.
【考点精析】根据题目的已知条件,利用正弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)若从这![]() 天中随机抽取两天,求至少有
天中随机抽取两天,求至少有![]() 天参加抽奖人数超过
天参加抽奖人数超过![]() 的概率;
的概率;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计若该活动持续
,并估计若该活动持续![]() 天,共有多少名顾客参加抽奖.
天,共有多少名顾客参加抽奖.
参考公式: 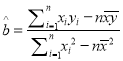 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点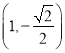 是椭圆
是椭圆![]() 上的点,离心率
上的点,离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 在椭圆
在椭圆![]() 上,若点
上,若点![]() 与点
与点![]() 关于原点对称,连接
关于原点对称,连接![]() 并延长与椭圆
并延长与椭圆![]() 的另一个交点为
的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该分店此次抽奖活动自开业始,持续![]() 天,参加抽奖的每位顾客抽到一等奖(价值
天,参加抽奖的每位顾客抽到一等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() ,抽到二等奖(价值
,抽到二等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() ,抽到三等奖(价值
,抽到三等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() .
.
试估计该分店在此次抽奖活动结束时送出多少元奖品?
参考公式: 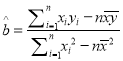 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2sin(﹣2x+ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位后,得到的图象对应的解析式应该是( )
个单位后,得到的图象对应的解析式应该是( )
A.y=﹣2sin(2x)
B.y=﹣2sin(2x+ ![]() )
)
C.y=﹣2sin(2x﹣ ![]() )
)
D.y=﹣2sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 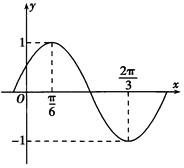
(1)求函数f(x)的解析式,并写出f(x)的单调减区间;
(2)已知△ABC的内角分别是A,B,C,A为锐角,且f( ![]() ﹣
﹣ ![]() )=
)= ![]() ,求cosA的值.
,求cosA的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com