
| A. | 15 | B. | 17 | C. | 24 | D. | 35 |
分析 【解法一】由平面向量的数量积运算化简$\overrightarrow{PA}$•$\overrightarrow{PB}$=${\overrightarrow{OP}}^{2}$-1,结合|$\overrightarrow{OP}$|的几何意义求出$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值.
【解法二】设出点A、B、P的坐标,利用坐标表示求出$\overrightarrow{PA}$•$\overrightarrow{PB}$,从而求出$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值.
【解法三】利用$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\frac{1}{4}$[${(\overrightarrow{PA}+\overrightarrow{PB})}^{2}$-${(\overrightarrow{PA}-\overrightarrow{PB})}^{2}$]=${|\overrightarrow{OP}|}^{2}$-1,结合题意求出$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值.
解答 解:【解法一】$\overrightarrow{PA}$•$\overrightarrow{PB}$=($\overrightarrow{OA}$-$\overrightarrow{OP}$)•($\overrightarrow{OB}$-$\overrightarrow{OP}$)
=$\overrightarrow{OA}$•$\overrightarrow{OB}$-$\overrightarrow{OP}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)+${\overrightarrow{OP}}^{2}$
=${\overrightarrow{OP}}^{2}$-1;
因为P在圆(x-4)2+(y-3)2=1上,
所以|$\overrightarrow{OP}$|≥4,
所以$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值为42-1=15.
【解法二】因为AB是圆x2+y2=1的一条直径,
故可设A(x0,y0),B(-x0,-y0),P(m,n),
$\overrightarrow{PA}$•$\overrightarrow{PB}$=(x0-m,y0-n)•(-x0-m,-y0-n)
=(m2+n2)-(${{x}_{0}}^{2}$+${{y}_{0}}^{2}$);
又${{x}_{0}}^{2}$+${{y}_{0}}^{2}$=1,
所以$\overrightarrow{PA}$•$\overrightarrow{PB}$=(m2+n2)-1;
又因为点P在圆(x-4)2+(y-3)2=1上,
所以|$\overrightarrow{OP}$|≥4,即m2+n2≥16,
所以$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值为15.
【解法三】由题意,得$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\frac{1}{4}$[${(\overrightarrow{PA}+\overrightarrow{PB})}^{2}$-${(\overrightarrow{PA}-\overrightarrow{PB})}^{2}$]=${|\overrightarrow{OP}|}^{2}$-1,
因为点P在圆(x-4)2+(y-3)2=1上,
所以|$\overrightarrow{OP}$|≥4,
所以$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值为15.
故选:A.
点评 本题考查了直线与圆的方程的应用问题,也考查了平面向量的数量积的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
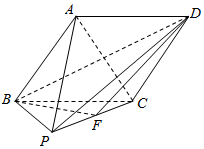 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6个 | B. | 9个 | C. | 12个 | D. | 24个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
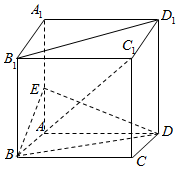 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为棱AA1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为棱AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com