
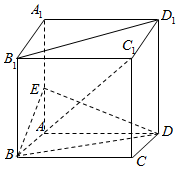
 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为棱AA1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为棱AA1的中点.分析 (1)通过证明B1D1⊥平面AA1C1得出AC1⊥B1D1;
(2)代入棱锥的体积公式计算即可.
解答 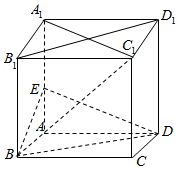 证明:(1)连接A1C1,
证明:(1)连接A1C1,
∵AA1⊥平面A1B1C1D1,B1D1?平面A1B1C1D1,
∴AA1⊥B1D1,
∵四边形A1B1C1D1是正方形,
∴A1C1⊥B1D1,
又AA1?平面AA1C1,A1C1?平面AA1C1,AA1∩A1C1=A1,
∴B1D1⊥平面AA1C1,∵AC1?平面AA1C1,
∴AC1⊥B1D1.
(2)VE-ABD=$\frac{1}{3}{S}_{△ABD}•EA$=$\frac{1}{3}×\frac{1}{2}×2×2×1$=$\frac{2}{3}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于基础题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-∞,1) | C. | (-∞,1] | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
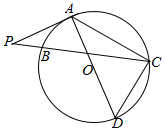 如图所示,已知⊙O的直径为AD,PA为⊙O的切线,由P作割线PBC依次交⊙O于B,C两点,且PA=CD=6,BC=9,AC=8.
如图所示,已知⊙O的直径为AD,PA为⊙O的切线,由P作割线PBC依次交⊙O于B,C两点,且PA=CD=6,BC=9,AC=8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 17 | C. | 24 | D. | 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{e}$-1 | B. | 2-$\frac{2}{e}$ | C. | 1+2e2 | D. | 1-$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com