
分析 (1)根据等比数列和等差数列的通项公式建立方程关系即可求数列{an}的通项公式
(2)求出数列{2an}的通项公式,即可求数列的前n项和Sn.
解答 解:(1)设公差为d,
∵a1=1,且a1,a3,a9成等比数列.
∴a32=a1a9,
即(1+2d)2=1×(1+8d),------(2分)
∴d=0(舍)或d=1,------(2分)
∴an=n------(1分)
(2)令bn=${2^{a_n}}={2^n}$------(1分)
∵$\frac{b_n}{{{b_{n-1}}}}=\frac{2^n}{{{2^{n-1}}}}=2$,为定常数
∴{bn}是以2为首项2为公比的等比数列------(2分)
∴Sn=$\frac{{2*(1-{2^n})}}{1-2}={2^{n+1}}-2$------(2分)
点评 本题主要考查数列通项公式以及数列求和的计算,根据条件建立方程关系求出d是解决本题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=μ$\overrightarrow{AC}$.
设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=μ$\overrightarrow{AC}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11π}{12}$ | B. | $\frac{π}{12}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
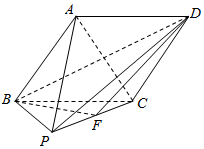 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
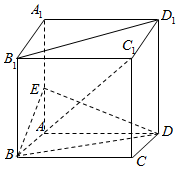 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为棱AA1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为棱AA1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com