
| A. | (0,1) | B. | (-∞,1) | C. | (-∞,1] | D. | (1,+∞) |
分析 求出f(x)的导数,问题转化为mex-x-m>0在x<0恒成立,构造函数g(x)=mex-x-m,(x<0),结合函数的单调性通过讨论m的范围确定函数的单调区间,求出m的具体范围即可.
解答 解:f′(x)=x(mex+1);
∴由不等式x2+(m+1)x>f′(x),
得,x2+(m+1)x>x(mex+1);
∵x<0;
∴mex-x-m>0;
令g(x)=mex-x-m,(x<0),
则g′(x)=mex-1,
当m≤1时,g(x)≤ex-1<0,
则g(x)在(-∞,0)递减,
∴g(x)>g(0)=0,符合题意,
m>1时,g(x)在(-∞,-lnm)递减,在(-lnm,0)递增,
∴g(x)min=g(-lnm)<g(0)=0,不合题意,
∴m的取值范围为(-∞,1];
故选:C.
点评 考查根据导数符号判断函数的单调性,及求函数的单调区间的方法,函数单调性定义的运用,根据导数求函数的极值及最值,根据函数单调性的定义求函数的最小值.


科目:高中数学 来源: 题型:解答题
 设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=μ$\overrightarrow{AC}$.
设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=μ$\overrightarrow{AC}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6个 | B. | 9个 | C. | 12个 | D. | 24个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
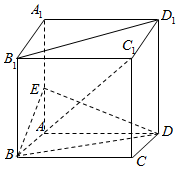 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为棱AA1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为棱AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com