
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他门各应偿还多少?该问题中,1斗为10升,则羊主人应偿还多少升粟?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,丙所得为( )
A.![]() 钱B.1钱C.
钱B.1钱C.![]() 钱D.
钱D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期,某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付,某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),绘制了如图所示的散点图:
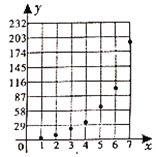
(I)根据散点图判断在推广期内,![]() 与
与![]() (c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(I)的判断结果求y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次.
参考数据:
|
|
|
|
|
|
|
4 | 62 | 1.54 | 2535 | 50.12 | 140 | 3.47 |
其中![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: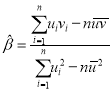 ,
,![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量AQI指数是反映空气质量状况指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值 |
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图所示的是某市11月1日至20日AQI指数变化的折线图:
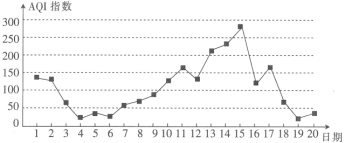
下列说法不正确的是( )
A.这![]() 天中空气质量为轻度污染的天数占
天中空气质量为轻度污染的天数占![]()
B.这![]() 天中空气质量为优和良的天数为
天中空气质量为优和良的天数为![]() 天
天
C.这![]() 天中AQI指数值的中位数略低于
天中AQI指数值的中位数略低于![]()
D.总体来说,该市11月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 与曲线
与曲线![]() 公共点的极坐标;
公共点的极坐标;
(2)设过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() ,以坐标原点O为极点,
,以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足|
于点M,点N为射线OM上的点,满足| ![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(1)①设动点![]() ,记
,记![]() 是直线
是直线![]() 的向上方向的单位方向向量,且
的向上方向的单位方向向量,且![]() ,以t为参数求直线
,以t为参数求直线![]() 的参数方程
的参数方程
②求曲线C的极坐标方程并化为直角坐标方程;
(2)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并与圆
外切并与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,问是否在
两点,问是否在![]() 轴上存在一点
轴上存在一点![]() ,使得当
,使得当![]() 变动时总有
变动时总有![]() ?若存在,请说明理由.
?若存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com