
【题目】近期,某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付,某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),绘制了如图所示的散点图:
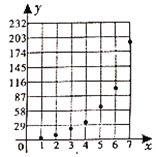
(I)根据散点图判断在推广期内,![]() 与
与![]() (c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(I)的判断结果求y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次.
参考数据:
|
|
|
|
|
|
|
4 | 62 | 1.54 | 2535 | 50.12 | 140 | 3.47 |
其中![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: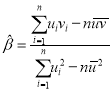 ,
,![]() 。
。
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 与椭圆
与椭圆![]() 的离心率相同.
的离心率相同.

(1)求![]() 的值;
的值;
(2)过椭圆![]() 的左顶点
的左顶点![]() 作直线
作直线![]() ,交椭圆
,交椭圆![]() 于另一点
于另一点![]() ,交椭圆
,交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在
在![]() 之间).①求
之间).①求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点);②设
为坐标原点);②设![]() 的中点为
的中点为![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,试探究点
,试探究点![]() 是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() 且与
且与![]() 轴相切,点
轴相切,点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,动点
,动点![]() 的轨迹记为
的轨迹记为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() :
:![]() 与曲线
与曲线![]() 交于点
交于点![]() 、
、![]() ;直线
;直线![]() :
:![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,其中
,其中![]() ,以
,以![]() 、
、![]() 为直径的圆
为直径的圆![]() 、
、![]() (
(![]() 、
、![]() 为圆心)的公共弦所在直线记为
为圆心)的公共弦所在直线记为![]() ,求
,求![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有A、B两种型号台灯,若购买2台A型台灯和6台B型台灯共需610元,若购买6台A型台灯和2台B型台灯共需470元.
(1)求A、B两种型号台灯每台分别多少元?
(2)采购员小红想采购A、B两种型号台灯共30台,且总费用不超过2200元,则最多能采购B型台灯多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中尝试进行课堂改革.现高一有![]() 两个成绩相当的班级,其中
两个成绩相当的班级,其中![]() 班级参与改革,
班级参与改革,![]() 班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过![]() 分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)是否有![]() 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
(2)按照分层抽样的方式从![]() 班中进步明显的学生中抽取
班中进步明显的学生中抽取![]() 人做进一步调查,然后从
人做进一步调查,然后从![]() 人中抽
人中抽![]() 人进行座谈,求这
人进行座谈,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: ,当
,当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关.
有关.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com