
【题目】已知矩形![]() ,将
,将![]() 沿矩形的对角线
沿矩形的对角线![]() 所在的直线进行翻折,在翻折过程中 ( )
所在的直线进行翻折,在翻折过程中 ( )
A. 存在某个位置,使得直线![]() 与直线
与直线![]() 垂直
垂直
B. 存在某个位置,使得直线![]() 与直线
与直线![]() 垂直
垂直
C. 存在某个位置,使得直线![]() 与直线
与直线![]() 垂直
垂直
D. 对任意位置,三对直线“![]() 与
与![]() ”,“
”,“![]() 与
与![]() ”,“
”,“![]() 与
与![]() ”均不垂直
”均不垂直
科目:高中数学 来源: 题型:
【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取![]() 个进行检查,测得每个球的直径(单位:
个进行检查,测得每个球的直径(单位:![]() ),将数据进行分组,得到如下频率分布表:
),将数据进行分组,得到如下频率分布表:
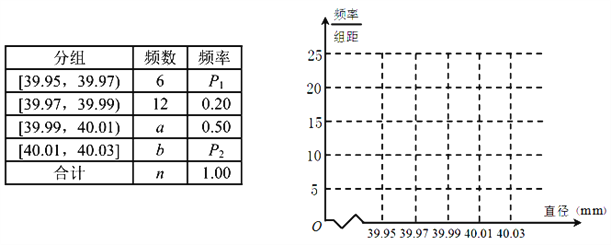
(1)求![]() 、
、![]() 、
、![]() 及
及![]() 、
、![]() 的值,并画出频率分布直方图(结果保留两位小数);
的值,并画出频率分布直方图(结果保留两位小数);
(2)已知标准乒乓球的直径为![]() ,且称直径在
,且称直径在![]() 内的乒乓球为五星乒乓球,若这批乒乓球共有
内的乒乓球为五星乒乓球,若这批乒乓球共有![]() 个,试估计其中五星乒乓球的数目;
个,试估计其中五星乒乓球的数目;
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表,试估计这批乒乓球直径的平均值和中位数.
)作为代表,试估计这批乒乓球直径的平均值和中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点,
的焦点,
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C的右焦点![]() 作直线l交椭圆C于A、B两点,交y轴于M点,若
作直线l交椭圆C于A、B两点,交y轴于M点,若![]()
![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校举办运动会时,高一(1)班有28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳和田径比赛的有3人,同时参加游泳和球类比赛的有3人,没有人同时参加三项比赛.则同时参加田径和球类比赛的人数是( ).
A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量![]() 和中位数;
和中位数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于4800元的概率
不少于4800元的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司过去五个月的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有下列对应数据:
(单位:万元)之间有下列对应数据:
| 2 | 4 | 5 | 6 | 8 |
|
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中![]() 的第一个数据丢失.已知
的第一个数据丢失.已知![]() 对
对![]() 呈线性相关关系,且回归方程为
呈线性相关关系,且回归方程为![]() ,则下列说法:①销售额
,则下列说法:①销售额![]() 与广告费支出
与广告费支出![]() 正相关;②丢失的数据(表中
正相关;②丢失的数据(表中![]() 处)为30;③该公司广告费支出每增加1万元,销售额一定增加
处)为30;③该公司广告费支出每增加1万元,销售额一定增加![]() 万元;④若该公司下月广告投入8万元,则销售
万元;④若该公司下月广告投入8万元,则销售
额为70万元.其中,正确说法有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com