
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
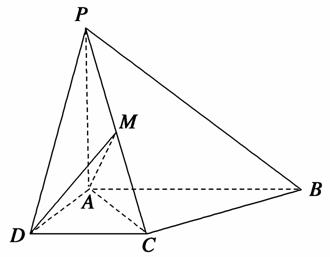
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥M-ACD的体积.
[证明] (1)由已知底面ABCD是直角梯形,AB∥DC,
又AB⊄平面PCD,CD⊂平面PCD,
∴AB∥平面PCD.
(2)在直角梯形ABCD中,过C作CE⊥AB于点E,则四边形ADCE为矩形,
∴AE=DC=1
又AB=2,∴BE=1,
在Rt△BEC中,∠ABC=45°,
∴CE=BE=1,CB= ,∴AD=CE=1,
,∴AD=CE=1,
则AC=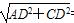 =
= ,AC2+BC2=AB2,
,AC2+BC2=AB2,
∴BC⊥AC.
又PA⊥平面ABCD,∴PA⊥BC,
又PA∩AC=A,∴BC⊥平面PAC.
(3)∵M是PC中点,
∴M到平面ADC的距离是P到平面ADC距离的一半.
∴VM-ACD=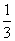 S△ACD·(
S△ACD·( PA)=
PA)=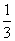 ×(
×( ×1×1)×
×1×1)× =
=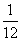 .
.


科目:高中数学 来源: 题型:
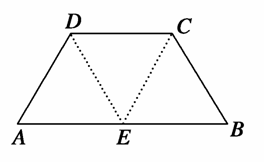
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
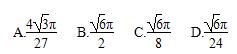
查看答案和解析>>
科目:高中数学 来源: 题型:
已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为________.
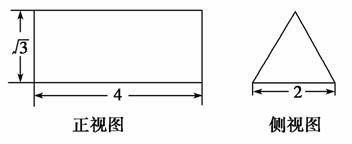
查看答案和解析>>
科目:高中数学 来源: 题型:
侧棱与底面垂直的棱柱称为直棱柱.已知直三棱柱ABC-A1B1C1的各顶点都在球O的球面上,且AB=AC=1,BC= ,若球O的体积为
,若球O的体积为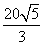 π,则这个直三棱柱的体积等于( )
π,则这个直三棱柱的体积等于( )
A.1 B.
C.2 D.
查看答案和解析>>
科目:高中数学 来源: 题型:
l1、l2、l3是空间三条不同的直线,则下列命题正确的是( )
A.l1⊥l2,l2⊥l3⇒l1∥l3
B.l1⊥l2,l2∥l3⇒l1⊥l3
C.l1∥l2∥l3⇒l1、l2、l3共面
D.l1、l2、l3共点⇒l1、l2、l3共面
查看答案和解析>>
科目:高中数学 来源: 题型:
在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是( )
A.BC∥平面PDF B.DF⊥平面PAE
C.平面PDF⊥平面ABC D.平面PAE⊥平面ABC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com