
【题目】函数f(x)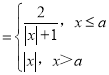 ,若任意t∈(a﹣1,a),使得f(t)>f(t+1),则实数a的取值范围为______.
,若任意t∈(a﹣1,a),使得f(t)>f(t+1),则实数a的取值范围为______.
【答案】1![]() a
a![]() 1
1
【解析】
根据f(x)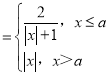 ,由t∈(a﹣1,a)t+1∈(a,a+1),得到f(t)
,由t∈(a﹣1,a)t+1∈(a,a+1),得到f(t)![]() ;f(t+1)=|t+1|;再根据任意t∈(a﹣1,a),使得f(t)>f(t+1),即
;f(t+1)=|t+1|;再根据任意t∈(a﹣1,a),使得f(t)>f(t+1),即![]() |t+1||t+1|(|t|+1)﹣2<0;然后分当t>0,﹣1≤t≤0,t<﹣1时,解不等式得
|t+1||t+1|(|t|+1)﹣2<0;然后分当t>0,﹣1≤t≤0,t<﹣1时,解不等式得![]() t
t![]() 1;根据若任意t∈(a﹣1,a),使得f(t)>f(t+1)成立,则(a﹣1,a)是(
1;根据若任意t∈(a﹣1,a),使得f(t)>f(t+1)成立,则(a﹣1,a)是(![]()
![]() 1)的子集求解.
1)的子集求解.
因为:f(x)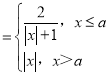 ,
,
由t∈(a﹣1,a)t+1∈(a,a+1),
∴f(t)![]() ;f(t+1)=|t+1|;
;f(t+1)=|t+1|;
∵任意t∈(a﹣1,a),使得f(t)>f(t+1),
∴![]() |t+1|
|t+1|![]() ;①
;①
当t>0时,①式转化为![]() 0<t
0<t![]() ;
;
当![]() 时①式转化为
时①式转化为![]()
![]() ,∴
,∴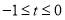 ;
;
t<﹣1时①式转化为![]() t2﹣3<0
t2﹣3<0![]() t<0;
t<0;
综上可得![]() t
t![]() 1;
1;
∵若任意t∈(a﹣1,a),使得f(t)>f(t+1),
∴a﹣1![]() 且a
且a![]() 1;
1;
∴1![]() a
a![]() 1;
1;


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知过椭圆![]() 的四个顶点与坐标轴垂直的四条直线围成的矩形
的四个顶点与坐标轴垂直的四条直线围成的矩形![]() (
(![]() 是第一象限内的点)的面积为
是第一象限内的点)的面积为![]() ,且过椭圆
,且过椭圆![]() 的右焦点
的右焦点![]() 的倾斜角为
的倾斜角为![]() 的直线过点
的直线过点![]() .
.
(1)求椭圆![]() 的标准方程
的标准方程
(2)若射线![]() 与椭圆
与椭圆![]() 的交点分别为
的交点分别为![]() .当它们的斜率之积为
.当它们的斜率之积为![]() 时,试问
时,试问![]() 的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解运动健身减肥的效果,某健身房调查了20名肥胖者,测量了他们的体重(单位:千克).健身之前他们的体重情况如三维饼图(1)所示,经过半年的健身后,他们的体重情况如三维饼图(2)所示,对比健身前后,关于这20名肥胖者,下面结论正确的是( )
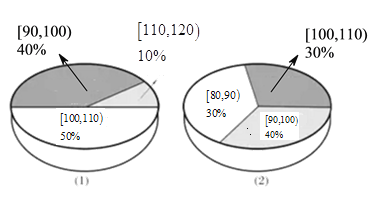
A.他们健身后,体重在区间![]() 内的人数不变
内的人数不变
B.他们健身后,体重在区间![]() 内的人数减少了2个
内的人数减少了2个
C.他们健身后,体重在区间![]() 内的肥胖者体重都有减轻
内的肥胖者体重都有减轻
D.他们健身后,这20位肥胖着的体重的中位数位于区间![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,点![]() 在曲线
在曲线![]() 上,直线l过点
上,直线l过点![]() 且与OM垂直,垂足为P.
且与OM垂直,垂足为P.
(1)当![]() 时,求在直角坐标系下点
时,求在直角坐标系下点![]() 坐标和l的方程;
坐标和l的方程;
(2)当M在C上运动且P在线段OM上时,求点P在极坐标系下的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备设计一个精美的心形巧克力盒子,它是由半圆![]() 、半圆
、半圆![]() 和正方形ABCD组成的,且
和正方形ABCD组成的,且![]() .设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,
.设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,![]() ,矩形EFGH的面积为
,矩形EFGH的面积为![]() .
.
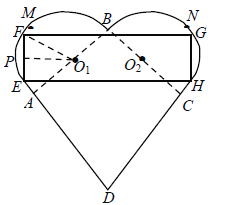
(1)写出S关于![]() 的函数关系式
的函数关系式![]()
(2)当![]() 为何值时矩形EFGH的面积最大?
为何值时矩形EFGH的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某中学甲、乙两班共有25名学生报名参加了一项 测试.这25位学生的考分编成的茎叶图,其中有一个数据因电脑操作员不小心删掉了(这里暂用x来表示),但他清楚地记得两班学生成绩的中位数相同.

(Ⅰ)求这两个班学生成绩的中位数及x的值;
(Ⅱ)如果将这些成绩分为“优秀”(得分在175分 以上,包括175分)和“过关”,若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛,求这3人中甲班至多有一人入选的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com