

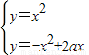 解得
解得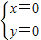 或
或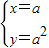 .
.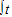 (-x2+2ax)dx-
(-x2+2ax)dx- t×t2+
t×t2+ (-t2+2at-t2)×(a-t)
(-t2+2at-t2)×(a-t) x3+ax2)|
x3+ax2)|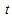 -
- t3+(-t2+at)×(a-t)=-
t3+(-t2+at)×(a-t)=- t3+at2-
t3+at2- t3+t3-2at2+a2t=
t3+t3-2at2+a2t= t3-at2+a2t.
t3-at2+a2t. t3-at2+a2t(0<t≤1).
t3-at2+a2t(0<t≤1). t2-2at+a2,令f′(t)=0,即
t2-2at+a2,令f′(t)=0,即 t2-2at+a2=0.解得t=(2-
t2-2at+a2=0.解得t=(2-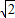 )a或t=(2+
)a或t=(2+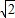 )a.
)a.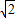 )a应舍去.
)a应舍去.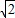 )a≥1,即a≥
)a≥1,即a≥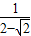 =
=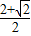 时,
时, .
.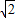 )a<1,即1<a<
)a<1,即1<a<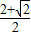 时,当0<t<(2-
时,当0<t<(2-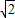 )a时f′(t)>0.当(2-
)a时f′(t)>0.当(2-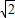 )a<t≤1时,f′(t)<0.
)a<t≤1时,f′(t)<0.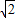 )a]上单调递增,在区间((2-
)a]上单调递增,在区间((2-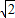 )a,1]上单调递减.
)a,1]上单调递减.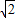 )a)=
)a)= [(2-
[(2-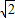 )a]3-a[(2-
)a]3-a[(2-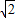 )a]2+a2(2-
)a]2+a2(2-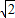 )a=
)a= a3.
a3.

科目:高中数学 来源: 题型:
 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=| 1 |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
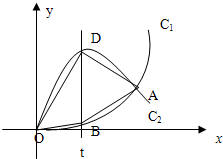
 (2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB.
(2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•黄冈模拟)如图,已知曲线c1:
(2009•黄冈模拟)如图,已知曲线c1:| x2 |
| a2 |
| y2 |
| b 2 |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
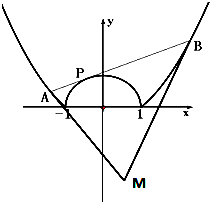 如图,已知曲线C1:x2+y2=1(|x|<1),C2:x2=8y+1(|x|≥1),动直线l与C1相切,与C2相交于A,B两点,曲线C2在A,B处的切线相交于点M.
如图,已知曲线C1:x2+y2=1(|x|<1),C2:x2=8y+1(|x|≥1),动直线l与C1相切,与C2相交于A,B两点,曲线C2在A,B处的切线相交于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com