
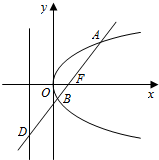
 已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.
已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.分析 (Ⅰ)设l:x=my+1,A(x1,y1),B(x2,y2),则联立方程化简可得y2-4my-4=0,从而可得$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1•x2+y1•y2=-3;
(Ⅱ)设M(a2,2a),则kMA=$\frac{{y}_{1}-2a}{{x}_{1}-{a}^{2}}$=$\frac{4}{{y}_{1}+2a}$,kMB=$\frac{4}{{y}_{2}+2a}$,kMD=$\frac{2a+\frac{2}{m}}{{a}^{2}+1}$,可得2×$\frac{2a+\frac{2}{m}}{{a}^{2}+1}$=$\frac{4}{{y}_{2}+2a}$+$\frac{4}{{y}_{1}+2a}$恒成立,从而可a2-1)(m+$\frac{1}{m}$)=0,即可求出点M的坐标.
解答 解:(Ⅰ)由题意知,抛物线y2=4x的焦点坐标为( 1,0),∴直线AB的方程为x=my+1(m≠0),
代入抛物线方程得y2-4my-4=0,
设A(x1,y1),B(x2,y2),
则y1+y2=4m,y1y2=-4,x1•x2=1,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1•x2+y1•y2=-3;
(Ⅱ)设M(a2,2a),
kMA=$\frac{{y}_{1}-2a}{{x}_{1}-{a}^{2}}$=$\frac{4}{{y}_{1}+2a}$,
同理,kMB=$\frac{4}{{y}_{2}+2a}$,kMD=$\frac{2a+\frac{2}{m}}{{a}^{2}+1}$,
∵直线MA,MD,MB的斜率始终成等差数列,
∴2×$\frac{2a+\frac{2}{m}}{{a}^{2}+1}$=$\frac{4}{{y}_{2}+2a}$+$\frac{4}{{y}_{1}+2a}$恒成立;
又∵y1+y2=4m,y1y2=-4,
∴(a2-1)(m+$\frac{1}{m}$)=0,
∴a=±1,
∴存在点M(1,2)或M(1,-2),使得对任意直线l,直线MA,MD,MB的斜率始终成等差数列.
点评 本题考查了直线与圆锥曲线的位置关系的应用,同时考查了学生的化简能力,属于中档题.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=2,AA′=4.给出下面五个命题:
在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=2,AA′=4.给出下面五个命题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | [1,3] | C. | (1,2] | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{3}$,则PC与平面PAD所成角的大小为45°.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{3}$,则PC与平面PAD所成角的大小为45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com