
分析 根据三角函数的单调性,和取得情况,求出函数的对称性和对称中心,结合函数奇偶性和单调性之间的关系分别进行判断即可.
解答 解:∵f(0)=f($\frac{2}{3}$),∴x=$\frac{0+\frac{2}{3}}{2}=\frac{1}{3}$是函数的一个对称轴,
故当x=$\frac{1}{3}$时,函数f(x)取得最值,故③正确,
∵f(0)=f($\frac{2}{3}$)=-f(1),
∴函数的一个对称中心为($\frac{5}{6}$,0),
∵f(x)在区间[$\frac{1}{3}$,1]上具有单调性,
∴函数的周期T=4($\frac{5}{6}-\frac{1}{3}$)=4×$\frac{1}{2}=2$,故①正确,
由①知函数的周期是2,x=$\frac{1}{3}$是函数的一个对称轴,
则函数在[$\frac{1}{3}$,$\frac{4}{3}$]上单调函数,在[$\frac{4}{3}$,$\frac{7}{3}$]上单调函数,故在[1,$\frac{5}{3}$]上不具有单调性,故②错误,
∵函数的一个对称中心为($\frac{5}{6}$,0),
∴将函数f(x)向左平移$\frac{5}{6}$个单位得到y=f(x+$\frac{5}{6}$),
此时函数关于原点对称,即y=f(x+$\frac{5}{6}$)是奇函数,故④正确,
⑤f(-$\frac{φ}{ω}$)=sin[ω(-$\frac{φ}{ω}$)+φ]=sin(-φ+φ)=0,
则当x=-$\frac{φ}{ω}$时,y=f(-$\frac{φ}{ω}$)+ω(-$\frac{φ}{ω}$)=0-φ=-φ,
即(-$\frac{φ}{ω}$,-φ)是y=f(x)+ωx图象的一个对称中心.故⑤正确,
故正确的是①③④⑤,
故答案为:①③④⑤
点评 本题主要考查与三角函数有关的命题的真假判断,根据条件求出函数的对称轴和对称中心是解决本题的关键.要求熟练掌握三角函数的图象和性质.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
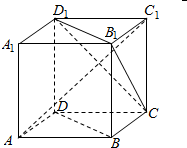
| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 平面ACC1A1⊥CB1D1 | D. | 异面直线AD与CB1所成的角为60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
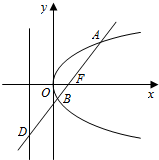 已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.
已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴为4,离心率e=$\frac{\sqrt{3}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴为4,离心率e=$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com