
分析 通过变形可得an+2+λan+1=(1+λ)(an+1+$\frac{1}{1+λ}$an),只需$\frac{1}{1+λ}$=λ,计算即得结论.
解答 解:由题意可知:an+2+λan+1=(1+λ)an+1+an=(1+λ)(an+1+$\frac{1}{1+λ}$an),
∴$\frac{1}{1+λ}$=λ,解得:λ=$\frac{-1+\sqrt{5}}{2}$或λ=$\frac{-1-\sqrt{5}}{2}$(舍),
∵a1=a2=1,∴a3=2,
易验证当n=1时满足题意,
故答案为:$\frac{-1+\sqrt{5}}{2}$.
点评 本题考查等比数列的概念,注意解题方法的积累,属于中档题.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [15°,90°] | B. | [60°,90°] | C. | [15°,105°] | D. | [30°,105°] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
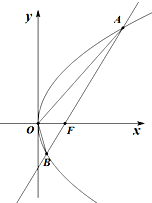 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
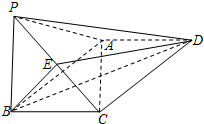 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com