
分析 (1)由中点坐标公式得到M(3,5),由已知得到点M′的坐标是($\sqrt{3}$,$\sqrt{5}$).
(2)求点M′的轨迹方程,根据范围确定路径的长度.
解答 解:(1)∵点M是线段AB的中点,由中点坐标公式,
∴M(3,5),由已知映射f:P(m,n)→P′($\sqrt{m}$,$\sqrt{n}$)(m≥0,n≥0),
∴点M′的坐标是($\sqrt{3}$,$\sqrt{5}$).
(2)设M′(x,y),则M(x2,y2),线段AB方程为:x+y=8(2≤x≤4)
∴对应点M′为x2+y2=8($\sqrt{2}$≤x≤2,2≤y≤$\sqrt{6}$),
∴路径为一段圆弧,圆心角为15°,
∴点M的对应点M′所经过的路线长度为8π×$\frac{15}{360}$=$\frac{π}{3}$.
点评 主要考查轨迹问题,曲线与方程的运用,学生的灵活应用能力与计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
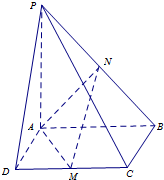 如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.
如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com