
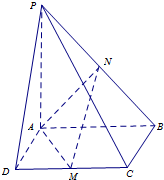
 如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.
如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.分析 (1)证明BC⊥面PAB,可得BC⊥AN,利用PA=AB,点N是PB的中点,可得AN⊥PB,即可证明AN⊥平面PBC;
(2)求二面角N-AM-B的余弦值,可采用找二面角的平面角的办法,因为易证平面PAB⊥平面ABCD,所以可以直接过N作AB的垂线垂足为G,则该垂线垂直于底面,然后过垂足G作AM的垂线GF,连接NF,则二面角的平面角找出,然后利用题目给出的条件,通过解直角三角形进行求解即可.
解答  (1)证明:∵PA⊥面ABCD,BC?面ABCD,∴PA⊥BC,
(1)证明:∵PA⊥面ABCD,BC?面ABCD,∴PA⊥BC,
∵ABCD为正方形,∴BC⊥AB;
又PA∩AB=A,
∴BC⊥面PAB,
∵AN?面PAB,
∴BC⊥AN,
∵PA=AB,点N是PB的中点,
∴AN⊥PB,
∵PB∩BC=B,
∴AN⊥平面PBC;
(2)解:取AB中点G,连结NG,则NG∥PA,PA⊥面ABCD,
∴NG⊥面ABCD.
∵AM?面ABCD,
∴NG⊥AM.
过G作GF⊥AM,垂足为F,连接NF,
∵NG∩GF=G,NG?面NGF,GF?面NGF,
∴AM⊥面NGF.
∵NF?面NGF,
∴AM⊥NF.
∴∠NFG是二面角N-AM-B的平面角.
在Rt△NGM中,MN=5,MG=AD=3,得NG=4,
在Rt△MGA中,AG=$\frac{3}{2}$,得AM=$\sqrt{M{G}^{2}+A{G}^{2}}$=$\frac{3\sqrt{5}}{2}$,GF=$\frac{AG•MG}{AM}$=$\frac{3\sqrt{5}}{5}$.
在Rt△NGF中,NF=$\sqrt{N{G}^{2}+G{F}^{2}}$=$\frac{\sqrt{445}}{5}$,
∴cos∠NFG=$\frac{GF}{NF}$=$\frac{3\sqrt{89}}{89}$.
∴二面角N-AM-B的余弦值为$\frac{3\sqrt{89}}{89}$.
点评 本题考查了线面垂直的判定,考查了二面角的平面角的求法,“寻找垂面,构造垂线”是找二面角的平面角常用的方法,此题是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,x02+2x0+2>0 | B. | ?x∈R,x2+2x+2≤0 | ||
| C. | ?x∈R,x2+2x+2>0 | D. | ?x∈R,x2+2x+2≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
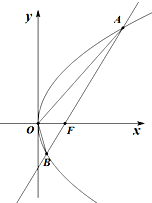 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | [1,3] | C. | (1,2] | D. | [2,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com