
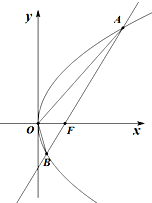
 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.分析 (Ⅰ)设直线AB的方程为y=k(x-$\frac{p}{2}$),代入抛物线,消x,利用y1y2=-4,求出p,即可求抛物线C的标准方程;
(Ⅱ)S△OAB=$\frac{1}{2}$×1×|y1-y2|,求△OAB的面积.
解答 解:(Ⅰ)F($\frac{p}{2}$,0),设直线AB的方程为y=k(x-$\frac{p}{2}$),…(2分)
代入抛物线,消x,得:ky2-2py-kp2=0,…(4分)
∴y1y2=-p2=-4,从而p=2,
∴抛物线C的方程为y2=4x. …(6分)
(Ⅱ)由已知,F(1,0),直线AB的方程为y=x-1,
代入抛物线,消x,得:y2-4y-4=0,
∴S△OAB=$\frac{1}{2}$×1×|y1-y2|=$\frac{1}{2}\sqrt{16+16}$=2$\sqrt{2}$…(15分)
点评 本题考查直线与抛物线的位置关系,考查三角形面积的计算,属于中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 0.046 | B. | 0.623 | C. | 0.977 | D. | 0.954 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
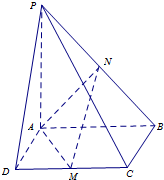 如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.
如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com