
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由已知可得:m∥n或为异面直线,即可判断出正误;
②由已知可得:m⊥n或相交或异面,即可判断出正误;
③根据线面垂直、面面平行的判定定理可知:α∥β,正确即可判断出正误;
④由已知可得:α⊥β或α∥β,即可判断出正误.
解答 解:①若α∥β,m?α,n?β,则m∥n或为异面直线,因此不正确;
②若α⊥β,m?α,n?β,则m⊥n或相交或异面,因此不正确;
③若m⊥α,n⊥β,m∥n,根据线面垂直、面面平行的判定定理可知:α∥β,正确;
④若m∥α,n∥β,m⊥n,则α⊥β或α∥β,因此不正确.
综上只有③是正确的,
故选:C.
点评 本题考查了线线、线面位置关系及其判定,考查了推理能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,x02+2x0+2>0 | B. | ?x∈R,x2+2x+2≤0 | ||
| C. | ?x∈R,x2+2x+2>0 | D. | ?x∈R,x2+2x+2≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
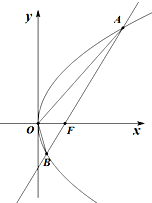 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1)、B(x2,y2)两点,且y1y2=-4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈R,均有x2-x+1>0”的否定是:“?x∈R,使得x2-x+1<0” | |
| B. | “x=3”是“2x2-7x+3=0”成立的充分不必要条件 | |
| C. | 若“p∧(¬q)”为真命题,则“p∧q”也为真命题 | |
| D. | 存在m∈R,使f(x)=(m-1)${x}^{{m}^{2}}$-4m+3是幂函数,且在(0,+∞)上是递增的 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=2,AA′=4.给出下面五个命题:
在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=2,AA′=4.给出下面五个命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com