
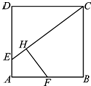
 如图所示,已知在边长为1的正方形ABCD的一边上取一点E,使AE=$\frac{1}{4}$AD,过AB的中点F作HF⊥EC于H.
如图所示,已知在边长为1的正方形ABCD的一边上取一点E,使AE=$\frac{1}{4}$AD,过AB的中点F作HF⊥EC于H. 分析 (1)建立直角坐标系.可得A(0,0),C(1,1),E(0,$\frac{1}{4}$),F($\frac{1}{2}$,0).利用相互垂直的直线斜率之间的关系可得直线FH的斜率,再利用点斜式分别得到直线CE、FH的方程,即可得到点H的坐标,利用两点间的距离公式即可得出答案.
(2)求出|EH|=$\sqrt{(\frac{1}{5})^{2}+(\frac{1}{4}-\frac{2}{5})^{2}}$=$\frac{1}{4}$,|CH|=$\sqrt{(1-\frac{1}{5})^{2}+(1-\frac{2}{5})^{2}}$=1,可得结论.
解答 解:(1)如图所示.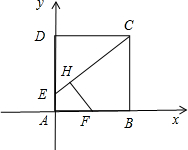 建立直角坐标系.
建立直角坐标系.
则A(0,0),C(1,1),E(0,$\frac{1}{4}$),F($\frac{1}{2}$,0)
直线CE:y=$\frac{1-\frac{1}{4}}{1-0}x+\frac{1}{4}$,化为y=$\frac{3}{4}x+\frac{1}{4}$.
∵FH⊥CE,∴kFH=-$\frac{4}{3}$.
∴直线FH:y=-$\frac{4}{3}$(x-$\frac{1}{2}$),即y=-$\frac{4}{3}$x+$\frac{2}{3}$.
联立解得H($\frac{1}{5}$,$\frac{2}{5}$).
∴|FH|=$\frac{1}{2}$,
∵|AF|=$\frac{1}{2}$,
∴|FH|=|AF|.
(2)∵|EH|=$\sqrt{(\frac{1}{5})^{2}+(\frac{1}{4}-\frac{2}{5})^{2}}$=$\frac{1}{4}$,|CH|=$\sqrt{(1-\frac{1}{5})^{2}+(1-\frac{2}{5})^{2}}$=1.
∴EH:HC=1:4.
点评 本题考查了通过建立直角坐标系证明几何问题、相互垂直的直线斜率之间的关系、点斜式、两点间的距离公式,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$f($\frac{π}{4}$)>$\sqrt{2}$f($\frac{π}{3}$) | B. | $\sqrt{2}$f($\frac{π}{6}$)>f($\frac{π}{4}$) | C. | $\sqrt{3}$f($\frac{π}{6}$)<f($\frac{π}{3}$) | D. | f(1)<2($\frac{π}{6}$)sin1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b⇒a2>b2 | B. | a>b⇒2a>2b | ||
| C. | a<b⇒$\frac{1}{a}$>$\frac{1}{b}$ | D. | 1<a<b⇒loga2<logb2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com