练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用数学归纳法证明“1+++…+＜n（n∈N*，n＞1）”时，由n=k（k＞1）不等式成立，推证n=k+1时，左边应增加的项数是（ ）

    A.2k﹣1 B.2k﹣1 C.2k D.2k+1

     

    C

    【解析】

    试题分析：考查不等式左侧的特点，分母数字逐渐增加1，末项为，然后判断n=k+1时增加的项数即可．

    【解析】
    左边的特点：分母逐渐增加1，末项为；

    由n=k，末项为到n=k+1，末项为=，∴应增加的项数为2k．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 2.2剩余类及其运算练习卷（解析版） 题型：填空题

    电子计算机中使用二进制，它与十进制的换算关系如下表：

    十进制

    1

    2

    3

    4

    5

    6

    …

    二进制

    1

    10

    11

    100

    101

    110

    …

     

    观察二进制1位数，2位数，3位数时，对应的十进制的数如上表，当二进制为6位数时能表示十进制数中最大的数是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 1.1整除练习卷（解析版） 题型：填空题

    （2013•宝山区一模）我们用记号“|”表示两个正整数间的整除关系，如3|12表示3整除12．试类比课本中不等关系的基本性质，写出整除关系的两个性质．① ；② ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例（解析版） 题型：解答题

    已知数列{an}的各项都是正数，且满足：．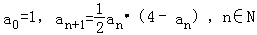

    （1）求a1，a2；

    （2）证明an＜an+1＜2，n∈N．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例（解析版） 题型：填空题

    用数学归纳法证明“（n+1）（n+2）…（n+n）=2n•1•2•…•（2n﹣1）”（n∈N+）时，从“n=k到n=k+1”时，左边应增添的式子是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷（解析版） 题型：选择题

    已知n为正偶数，用数学归纳法证明1﹣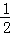+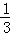﹣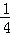+…+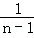=2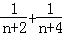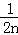（+…+）时，若已假设n=k（k≥2为偶数）时命题为真，则还需要用归纳假设再证（ ）

    A.n=k+1时等式成立 B.n=k+2时等式成立

    C.n=2k+2时等式成立 D.n=2（k+2）时等式成立

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷（解析版） 题型：选择题

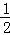
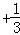
    证明1+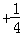+…+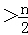（n∈N*），假设n=k时成立，当n=k+1时，左端增加的项数是（ ）

    A.1项 B.k﹣1项 C.k项 D.2k项

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.2一般形式柯西不等式练习卷（解析版） 题型：填空题

    （2014•辽宁）对于c＞0，当非零实数a，b满足4a2﹣2ab+b2﹣c=0且使|2a+b|最大时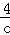，++的最小值为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明“方程ax2+bx+c=0（a≠0）至多有两个解”的假设中，正确的是（ ）

    A.至多有一个解 B.有且只有两个解

    C.至少有三个解 D.至少有两个解

     

    查看答案和解析>>

    同步练习册答案