
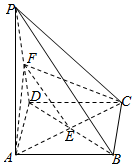
 底面为正方形的四棱锥P-ABCD,F为PD中点.
底面为正方形的四棱锥P-ABCD,F为PD中点.分析 (1)根据线面平行的判定定理证明PB∥EF即可证明PB∥平面EAC;
(2)由PD⊥面ABCD,可证PD⊥AC,又可证AC⊥BD,利用线面垂直的判定定理即可证明AC⊥面PBD.
解答 (本题满分为12分)
证明:(1)∵四边形ABCD为正方形,
∴E为BD中点.
∵F为棱PD中点
∴PB∥EF.…(3分)
∵PB?平面ACF,EF?平面ACF,
∴直线PB∥平面ACF. …(6分)
(2)∵PD⊥面ABCD,AC?平面ABCD,
∴PD⊥AC,
又∵正方形ABCD中,有AC⊥BD,且PD∩BD=D,
∴AC⊥面PBD.…(12分)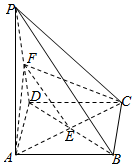
点评 本题主要考查空间直线和平面平行以及直线和平面垂直的判定,要求熟练掌握相应的判定定理,考查了空间想象能力和推理论证能力,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{52π}{3}$ | B. | $\frac{44π}{3}$ | C. | 16π | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
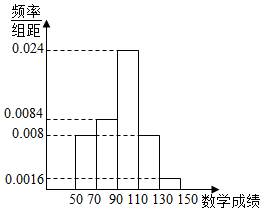 语文成绩服从正态分布N(100,17.52),数学成绩的频率分布直方图如图,如果成绩大于135的则认为特别优秀.
语文成绩服从正态分布N(100,17.52),数学成绩的频率分布直方图如图,如果成绩大于135的则认为特别优秀.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}+\frac{1}{2}i$ | B. | $-\frac{3}{2}-\frac{1}{2}i$ | C. | $\frac{3}{2}+\frac{1}{2}i$ | D. | $\frac{3}{2}-\frac{1}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,5,2) | B. | (3,-5,2) | C. | (3,-5,-2) | D. | (-3,-5,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com