
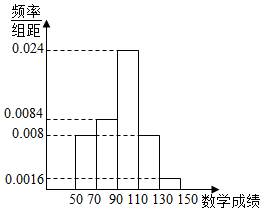
 语文成绩服从正态分布N(100,17.52),数学成绩的频率分布直方图如图,如果成绩大于135的则认为特别优秀.
语文成绩服从正态分布N(100,17.52),数学成绩的频率分布直方图如图,如果成绩大于135的则认为特别优秀.分析 (1)先求出语文成绩特别优秀的概率和数学成绩特别优秀的概率,由此能求出语文和数学两科都特别优秀的人的个数.
(2)由题意X的所有可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(1)∵语文成绩服从正态分布N(100,17.52),
∴语文成绩特别优秀的概率为p1=P(X≥135)=(1-0.96)×$\frac{1}{2}$=0.02,
数学成绩特别优秀的概率为p2=0.0016×$20×\frac{3}{4}$=0.024,
∴语文特别优秀的同学有500×0.02=10人,
数学特别优秀的同学有500×0.024=12人.
(2)语文数学两科都优秀的有6人,单科优秀的有10人,
X的所有可能取值为0,1,2,3,
P(X=0)=$\frac{{C}_{10}^{3}}{{C}_{16}^{3}}$=$\frac{3}{14}$,
P(X=1)=$\frac{{C}_{10}^{2}{C}_{6}^{1}}{{C}_{16}^{3}}$=$\frac{27}{56}$,
P(X=2)=$\frac{{C}_{10}^{1}{C}_{6}^{2}}{{C}_{16}^{3}}$=$\frac{15}{56}$,
P(X=3)=$\frac{{C}_{6}^{3}}{{C}_{16}^{3}}$=$\frac{1}{28}$,
∴X的分布列为:
| x | 0 | 1 | 2 | 3 |
| P | $\frac{3}{14}$ | $\frac{27}{56}$ | $\frac{15}{56}$ | $\frac{1}{28}$ |
点评 本题考查正态分布的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{{2\sqrt{15}}}{3}$ | D. | $\frac{{\sqrt{15}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [1,2] | C. | [0,1] | D. | (-∞,1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{3}$π | B. | $\frac{25}{2}$π | C. | $\frac{83}{3}$π | D. | $\frac{83}{2}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com