练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．设集合A={x|lgx＞0}，B={x|2＜2x＜8}，则（　　）
    A．A=BB．A⊆BC．A?BD．A∩B=∅

    分析 先根据函数的单调性分别解对数不等式和指数不等式，将集合A、B化简，再根据集合的关系可得本题的答案．

    解答 解：对于集合A，lgx＞0得x＞1，所以A={x|x＞1}，
    而集合B，解不等式2＜2x＜8，得1＜x＜3，
    ∴B={x|1＜x＜3}，
    ∴A?B．
    故选：C．

    点评 本题给出含有指数和对数的不等式构成的集合，求集合的关系，着重考查了指、对数不等式的解法和集合的关系等知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．要完成下列3项抽样调查：
    ①从15瓶饮料中抽取5瓶进行食品卫生检查．
    ②某校报告厅有25排，每排有38个座位，有一次报告会恰好坐满了学生，报告会结束后，为了听取意见，需要抽取25名学生进行座谈．
    ③某中学共有240名教职工，其中一般教师180名，行政人员24名，后勤人员36名．为了了解教职工对学校在校务公开方面的意见，拟抽取一个容量为20的样本．
    较为合理的抽样方法是（　　）
    A．①简单随机抽样，②系统抽样，③分层抽样
    B．①简单随机抽样，②分层抽样，③系统抽样
    C．①系统抽样，②简单随机抽样，③分层抽样
    D．①分层抽样，②系统抽样，③简单随机抽样

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若直线的参数方程为$\left\{\begin{array}{l}x=1+\sqrt{3}t\\ y=3-3t\end{array}\right.$（t为参数），则直线的倾斜角为（　　）
    A．30°B．60°C．120°D．150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．某媒体对“男女延迟退休”这一公众关注的问题进行名意调查，如表是在某单位得到的数据：
     赞同  反对合计
    男50 150200
    女30 170 200
    合计 80320 400
    （Ⅰ）能否有97.5%的把握认为对这一问题的看法与性别有关？
    （Ⅱ）从赞同“男女延迟退休”的80人中，利用分层抽样的方法抽出8人，然后从中选出3人进行陈述发言，设发言的女士人数为X，求X的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．若x=2是函数f（x）=x（x-m）2的极大值点，则m的值为（　　）
    A．3B．6C．2或6D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知集合A={x|x-a＜0}，B={x|x2-2x-3＜0}，若B⊆A，则实数a的取值范围是a≥3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知实数x，y满足不等式$\left\{{\begin{array}{l}{x-y+1≥0}\\{x+y-2≤0}\\{y≥0}\end{array}}\right.$，则z=2x-y的最大值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．三棱锥S-ABC中，△SAB和△ABC是边长为2$\sqrt{3}$的正三角形，二面角S-AB-C的平面角为60°，若S，A，B，C都在同一个球面上，则该球的表面积为（　　）
    A．$\frac{52π}{3}$B．$\frac{44π}{3}$C．16πD．20π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

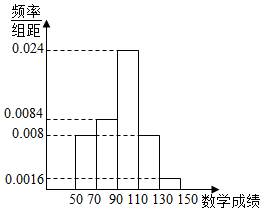    2．语文成绩服从正态分布N（100，17.52），数学成绩的频率分布直方图如图，如果成绩大于135的则认为特别优秀．
    （1）这500名学生中本次考试语文、数学特别优秀的大约各多少人？
    （2）如果语文和数学两科都特别优秀的共有6人，
    从（1）中的这些同学中随机抽取3人，设三人中两科都特别优秀的有x人，求x的分布列和数学期望．（附公式及表）
    若x～N（μ，σ2），则P（μ-σ＜x≤μ+σ）=0.68，P（μ-2σ＜x≤μ+2σ）=0.96．

    查看答案和解析>>

    同步练习册答案