
| A. | 2 | B. | 1 | C. | $\frac{{2\sqrt{15}}}{3}$ | D. | $\frac{{\sqrt{15}}}{3}$ |
分析 由正弦定理化简已知等式,代入余弦定理可求cosC的值,利用同角三角函数基本关系式可求sinC的值,根据基本不等式可求ab的最大值,进而利用三角形面积公式即可得解△ABC面积的最大值.
解答 解:由正弦定理得:$a(a-\frac{1}{2}b)={c^2}-{b^2}$,即${a^2}+{b^2}-{c^2}=\frac{1}{2}ab$,
代入余弦定理得:$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=\frac{{\frac{1}{2}ab}}{2ab}=\frac{1}{4}$,
所以:$sinC=\sqrt{1-{{(\frac{1}{4})}^2}}=\frac{{\sqrt{15}}}{4}$,
又:由${a^2}+{b^2}-{c^2}=\frac{1}{2}ab$,c=2,
得:${a^2}+{b^2}=\frac{1}{2}ab+4≥2ab$,
解得:$ab≤\frac{8}{3}$,
所以:△ABC面积为$S=\frac{1}{2}absinC=\frac{1}{2}•\frac{{\sqrt{15}}}{4}•ab=\frac{{\sqrt{15}}}{8}•ab≤\frac{{\sqrt{15}}}{8}×\frac{8}{3}=\frac{{\sqrt{15}}}{3}$,
当且仅当$a=b=\frac{{2\sqrt{6}}}{3}$时等号成立,
故△ABC面积的最大值为$\frac{{\sqrt{15}}}{3}$,
故选:D.
点评 本题主要考查了正弦定理,余弦定理,同角三角函数基本关系式,基本不等式,三角形面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
| 赞同 | 反对 | 合计 | |
| 男 | 50 | 150 | 200 |
| 女 | 30 | 170 | 200 |
| 合计 | 80 | 320 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{52π}{3}$ | B. | $\frac{44π}{3}$ | C. | 16π | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-9] | B. | [0,2] | C. | (-∞,-9]∪[0,2] | D. | [-9,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$-$\frac{4}{5}$i | B. | $\frac{3}{5}$+$\frac{4}{5}$i | C. | $\frac{4}{5}$-$\frac{3}{5}$i | D. | $\frac{4}{5}$+$\frac{3}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
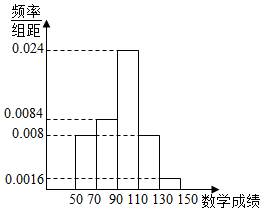 语文成绩服从正态分布N(100,17.52),数学成绩的频率分布直方图如图,如果成绩大于135的则认为特别优秀.
语文成绩服从正态分布N(100,17.52),数学成绩的频率分布直方图如图,如果成绩大于135的则认为特别优秀.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com