
分析 (Ⅰ)运用向量的数量积的坐标表示,结合正弦定理和两角和的正弦公式,即可求得A;
(Ⅱ)运用正弦定理求得sinB,由A>B,可得cosB,运用两角和的正弦公式可得sin∠ADC,再由正弦定理,计算即可得到所求值.
解答 解:(Ⅰ)由$\overrightarrow{m}$=(cos A,cos C),$\overrightarrow{n}$=(c,a),$\overrightarrow{p}$=(2b,0),
可得$\overrightarrow{m}$•($\overrightarrow{n}$-$\overrightarrow{p}$)=(cosA,cosC)•(c-2b,a)=(c-2b)cosA+acosC=0,
由正弦定理,可得(sinC-2sinB)cosA+sinAcosC=0,
即为2sinBcosA=sinCcosA+cosCsinA=sin(C+A)=sinB,
由sinB≠0,可得cosA=$\frac{1}{2}$,
由0<A<π,可得A=$\frac{π}{3}$;
(Ⅱ)由$\frac{a}{sinA}$=$\frac{b}{sinB}$,a=2,b=1,A=$\frac{π}{3}$,
可得sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}}{4}$,
由a>b,可得A>B,则cosB=$\sqrt{1-\frac{3}{16}}$=$\frac{\sqrt{13}}{4}$,
在△ACD中,sin∠ADC=sin(π-∠DCA-$\frac{π}{3}$)
=sin(∠DCA+$\frac{π}{3}$)=sin(B+$\frac{π}{3}$)=$\frac{1}{2}$sinB+$\frac{\sqrt{3}}{2}$cosB
=$\frac{1}{2}$×$\frac{\sqrt{3}}{4}$+$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{13}}{4}$=$\frac{\sqrt{3}+\sqrt{39}}{8}$,
在△ACD中,由正弦定理,可得:
CD=$\frac{ACsin\frac{π}{3}}{sin∠ADC}$=$\frac{\sqrt{3}}{2}$×$\frac{8}{\sqrt{3}+\sqrt{39}}$=$\frac{\sqrt{13}-1}{3}$.
点评 本题考查向量数量积的坐标表示和三角函数的恒等变换,以及三角形的正弦定理的运用,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$-$\frac{4}{5}$i | B. | $\frac{3}{5}$+$\frac{4}{5}$i | C. | $\frac{4}{5}$-$\frac{3}{5}$i | D. | $\frac{4}{5}$+$\frac{3}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
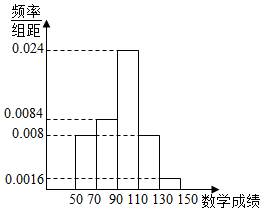 语文成绩服从正态分布N(100,17.52),数学成绩的频率分布直方图如图,如果成绩大于135的则认为特别优秀.
语文成绩服从正态分布N(100,17.52),数学成绩的频率分布直方图如图,如果成绩大于135的则认为特别优秀.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在区间[-$\frac{π}{12}$,$\frac{5}{12}$π]上单调递增 | B. | 在区间[$\frac{π}{4},\frac{π}{4}$]上单调递增 | ||
| C. | 在区间[$\frac{π}{4}$,$\frac{3π}{4}$]上单调递减 | D. | 在区间[-$\frac{π}{12}$,$\frac{5}{12}$π]上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}+\frac{1}{2}i$ | B. | $-\frac{3}{2}-\frac{1}{2}i$ | C. | $\frac{3}{2}+\frac{1}{2}i$ | D. | $\frac{3}{2}-\frac{1}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<-2或m>-1 | B. | -2<m<0 | C. | -2<m<-1 | D. | m>-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com