练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．当m=1时，复数z=$\frac{1+i}{m-2i}$的虚部为（　　）
    A．$-\frac{1}{5}$B．$\frac{1}{5}$C．$-\frac{3}{5}$D．$\frac{3}{5}$

    分析 直接把m=1代入复数z，再由复数代数形式的乘除运算化简即可得答案．

    解答 解：当m=1时，z=$\frac{1+i}{m-2i}$=$\frac{1+i}{1-2i}=\frac{（1+i）（1+2i）}{（1-2i）（1+2i）}=\frac{-1+3i}{5}$=$-\frac{1}{5}+\frac{3}{5}i$，
    ∴复数z=$\frac{1+i}{m-2i}$的虚部为：$\frac{3}{5}$．
    故选：D．

    点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．若x=2是函数f（x）=x（x-m）2的极大值点，则m的值为（　　）
    A．3B．6C．2或6D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．为了了解大学生观看某电视节目是否与性别有关，一所大学心理学教师从该校学生中随机抽取了50人进行问卷调查，得到了如下的列联表，若该教师采用分层抽样的方法从50份问卷调查中继续抽查了10份进行重点分析，知道其中喜欢看该节目的有6人．
      喜欢看该节目 不喜欢看该节目 合计
     女生  5 
     男生 10  
     合计   50
    （1）请将上面的列联表补充完整；
    （2）是否有99.5%的把握认为喜欢看该节目与性别有关？说明你的理由；
    （3）已知喜欢看该节目的10位男生中，A1、A2、A3、A4、A5还喜欢看新闻，B1、B2、B3还喜欢看动画片，C1、C2还喜欢看韩剧，现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查，求B1和C1不全被选中的概率．
    下面的临界值表供参考：
     P（K2≥k） 0.15 0.10 0.05 0.025 0.010 0.0050． 001
     k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
    （参考公式：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知i为虚数单位，则复数$\frac{{1-\frac{1}{2}i}}{{1+\frac{1}{2}i}}$=（　　）
    A．$\frac{3}{5}$-$\frac{4}{5}$iB．$\frac{3}{5}$+$\frac{4}{5}$iC．$\frac{4}{5}$-$\frac{3}{5}$iD．$\frac{4}{5}$+$\frac{3}{5}$i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．函数f（x）=ln（5x-125）的定义域为（3，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

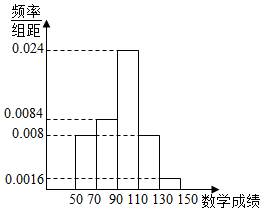    2．语文成绩服从正态分布N（100，17.52），数学成绩的频率分布直方图如图，如果成绩大于135的则认为特别优秀．
    （1）这500名学生中本次考试语文、数学特别优秀的大约各多少人？
    （2）如果语文和数学两科都特别优秀的共有6人，
    从（1）中的这些同学中随机抽取3人，设三人中两科都特别优秀的有x人，求x的分布列和数学期望．（附公式及表）
    若x～N（μ，σ2），则P（μ-σ＜x≤μ+σ）=0.68，P（μ-2σ＜x≤μ+2σ）=0.96．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．将函数y=3sin（2x+$\frac{π}{3}$）的图象向右平移$\frac{π}{3}$个单位长度，所得图象对应的函数（　　）
    A．在区间[-$\frac{π}{12}$，$\frac{5}{12}$π]上单调递增B．在区间[$\frac{π}{4}，\frac{π}{4}$]上单调递增
    C．在区间[$\frac{π}{4}$，$\frac{3π}{4}$]上单调递减D．在区间[-$\frac{π}{12}$，$\frac{5}{12}$π]上单调递减

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．⊙Ox2+y2=25的圆心O到直线3x+4y+5=0的距离等于（　　）
    A．1B．3C．5D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．数列{an}中，a1=1，Sn为数列{an}的前n项和，且对?n≥2，都有$\frac{2{a}_{n}}{{a}_{n}{S}_{n}-{S}_{n}^{2}}$=1．则{an}的通项公式an=$\left\{\begin{array}{l}{1，n=1}\\{\frac{-2}{n（n+1）}，n≥2}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案