
【题目】设公差大于0的等差数列![]() 的前
的前![]() 项和为
项和为![]() .已知
.已知![]() ,且
,且![]() 成等比数列,记数列
成等比数列,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求![]() ;
;
(2)若对于任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ) ![]() .
.
【解析】试题分析:
(1)利用条件解方程组求出首项和公差,即可写出通项公式,再利用裂项法求和;
(2)写出不等式,分离参数后,转化为求关于n的函数的最小值,利用均值不等式即可求出.
试题解析:
(Ⅰ)设{an}的公差为d(d>0),
由S3=15有3a1+![]() =15,化简得a1+d=5,①
=15,化简得a1+d=5,①
又∵ a1,a4,a13成等比数列,
∴ a42=a1a13,即(a1+3d)2=a1(a1+12d),化简3d=2a1,②
联立①②解得a1=3,d=2,
∴ an=3+2(n-1)=2n+1. ∴ ![]() ,
,
∴ ![]() .
.
(Ⅱ) ∵ ![]() +11,即
+11,即![]() ,
,
∴ ![]() ,又
,又![]() ≥6 ,
≥6 ,
当且仅当n=3时,等号成立,
∴ ![]() ≥162, ∴
≥162, ∴ ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知点P是圆F1:(x﹣1)2+y2=8上任意一点,点F2与点F1关于原点对称,线段PF2的垂直平分线分别与PF1,PF2交于M,N两点.
(1)求点M的轨迹C的方程;
(2)过点G(0, ![]() )的动直线l与点的轨迹C交于A,B两点,在y轴上是否存在定点Q,使以AB为直径的圆恒过这个点?若存在,求出点Q的坐标;若不存在,请说明理由.
)的动直线l与点的轨迹C交于A,B两点,在y轴上是否存在定点Q,使以AB为直径的圆恒过这个点?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C为锐角△ABC的内角, ![]() =(sinA,sinBsinC),
=(sinA,sinBsinC), ![]() =(1,﹣2),
=(1,﹣2), ![]() ⊥
⊥ ![]() .
.
(1)tanB,tanBtanC,tanC能否构成等差数列?并证明你的结论;
(2)求tanAtanBtanC的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2 ![]() ,PA=4且E为PB的中点.
,PA=4且E为PB的中点. 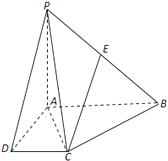
(1)求证:CE∥平面PAD;
(2)求直线CE与平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数 ![]() 在(0,+∞)上为增函数,g(x)=f(x)+2
在(0,+∞)上为增函数,g(x)=f(x)+2 ![]()
(1)求m的值,并确定f(x)的解析式;
(2)对于任意x∈[1,2],都存在x1 , x2∈[1,2],使得f(x)≤f(x1),g(x)≤g(x2),若f(x1)=g(x2),求实数t的值;
(3)若2xh(2x)+λh(x)≥0对于一切x∈[1,2]成成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y= ![]() cosx的图象,需将函数y=
cosx的图象,需将函数y= ![]() sin(2x+
sin(2x+ ![]() )的图象上所有的点的变化正确的是( )
)的图象上所有的点的变化正确的是( )
A.横坐标缩短到原来的 ![]() 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动 ![]() 个单位长度
个单位长度
B.横坐标缩短到原来的 ![]() 倍(纵坐标不变),再向右平行移动
倍(纵坐标不变),再向右平行移动 ![]() 个单位长度
个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动 ![]() 个单位长度
个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值ξ(元)的概率分布列和期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴正半轴为极轴且取相同的单位长度建立极坐标系.已知点
轴正半轴为极轴且取相同的单位长度建立极坐标系.已知点![]() 的参数方程为
的参数方程为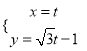 (
(![]() 为参数),点
为参数),点![]() 在曲线
在曲线![]() 上.
上.
(1)求在平面直角坐标系![]() 中点
中点![]() 的轨迹方程和曲线
的轨迹方程和曲线![]() 的普通方程;
的普通方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com